由本章第3、4两节的分析可知，若要解决同时考虑单箱重量与订舱数量差别定价的博弈问题，相应的博弈模型将变得非常复杂。因此，为便于问题阐述，本节仍只考虑两家企业竞争的情形。

如果同时考虑竞争环境下的单箱重量与订舱数量差别定价模型，则本章第4节中的集装箱的公布价格p即可以视为针对集装箱单箱重量进行分类后的二部总运价，即p可以通过p=p 0+p i的形式表达。因此，结合本章第3、4两节的相关阐述易知，两家企业的价格函数可以分别表达为P 1（p 0（1），p i（1），δi（1），θj（1），γj（1））及P 2（p 0（2），p i（2），δi（2），θj（2），γj（2））。

此时决策变量共有2×2组各3个，因此也相应地假设2×2组各3个，即共12个替代系数，分别为d 1（11），d 1（12），d 1（13）；d 2（11），d 2（12），d 2（13）；d 1（21），d 1（22），d 1（23）；d 2（21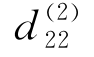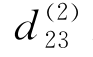），，。(www.daowen.com)

至此，同时考虑单箱重量与订舱数量差别定价的博弈问题也可用与本章第3、4节原理相似的静态及动态博弈模型加以解决。与前述两节唯一的不同之处在于，若同时考虑单箱重量与订舱数量差别定价，只需相应增加博弈模型涉及的变量个数即可。可以发现，就模型原理而言，考虑多因素影响的差别定价博弈问题与仅考虑单一因素的差别定价博弈问题并没有实质性的区别。

也就是说，本章前述的各博弈模型有着非常优越的可扩展性。当然，随着考虑因素的逐步增加，在实际应用中，确定各因素对需求量的具体影响程度并通过函数表示，将变得更加困难，但此类困难是在设计多维差别定价方案过程中所不可避免的，与博弈模型本身并无太多关联。