由本书第3章的相关研究可知，理论上，基于集装箱单箱重量的差别定价模型可以用以下函数形式表示：

式中，p 0为班轮公司的针对所有重量集装箱的基准费率；w为集装箱单箱重量；w i-1与w i分别为第i重量等级的上下限；w max为集装箱单箱重量的技术额定上限；p i（0≤p 1＜p 2＜…＜p i＜…＜p m）为相应区间的“偏重箱附加费率”。上式即表示当某集装箱单箱重量w超过w i-1，但不超过w i时，应在基准运费p的基础上，额外支付“偏重箱附加费”p i。若将区间（w i-1，w i]表示为Δi，则式（6-23）也可表达为

正如本书第3章所述，与通常意义上的优化模型不同，该模型的决策变量除了各区间的折扣率之外，每一个订舱量区间的具体范围也需要通过科学决策来加以确定，即基于订舱量的数量折扣价格函数可以表达为P（p 0，p 1，w，Δ1；p 0，p 2，w，Δ2；…；p 0，p i，w，Δi；…p 0，p m，w，Δm），定义映射T 1i：Δi→δi，因此上述价格函数可进一步表达为P（p 0，p 1，w，δ1；p 0，p 2，w，δ2；…p 0，p i，w，δi；…p 0，p m，w，δm）。尽管集装箱单箱重量的实际数值是由托运方决定的，但班轮公司可以通过合理制定二部定价方案诱导托运人调整其装箱配货决策，从而使得投入运输的集装箱的重量结构更趋合理，因此该价格函数可进一步简单表示为P（p 0，p 1，δ1；p 0，p 2，δ2；…p 0，p i，δi；…p 0，p m，δm），为表达方便，以下简写为P（p 0，p i，δi）。(www.daowen.com)

不考虑竞争影响时，对于某特定企业k而言，其需求量Q是其所制定的价格P的函数，而P又是p 0，p i，δi的函数，因此可知Q也表示为p 0，p i，δi的函数，不妨假设Q=f 1（p 0，p i，δi）。

为简化问题描述，本节假设只有两家企业，即班轮公司1与班轮公司2，其价格分别为P 1、P 2，可分别表达为P 1（p 0（1），p i（1），δi（1））和P 2（p 0（2），p i（2），δi（2））。考虑到此时决策变量有两组各三个，因此也相应地假设两组各三个替代系数，即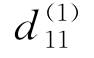，d 1（12），d 1（13）；d 2（11），d 2（12），d 2（13）。