1）r取0.03、0.04、0.05

当r取0.03、0.04、0.05，即μ＞r时，相应的期权应为认沽期权，具体P*的取值及P*取值与σ、μ的关系图如表5-4、表5-5、表5-6及图5-1、图5-2、图5-3所示。

（1）r=0.03。

表5-4　r=0.03时P*的取值

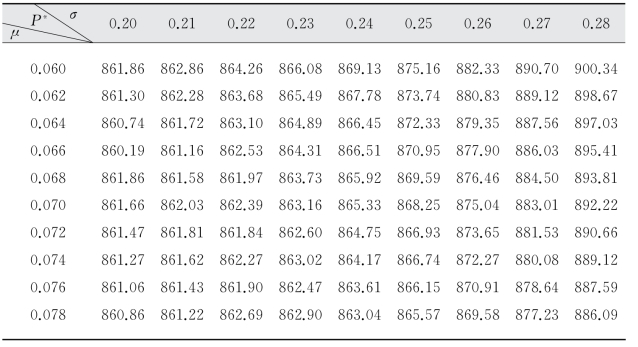
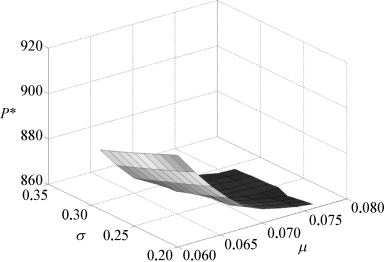
图5-1　r=0.03时P*取值与σ、μ的关系

（2）r=0.04。

表5-5　r=0.04时P*的取值

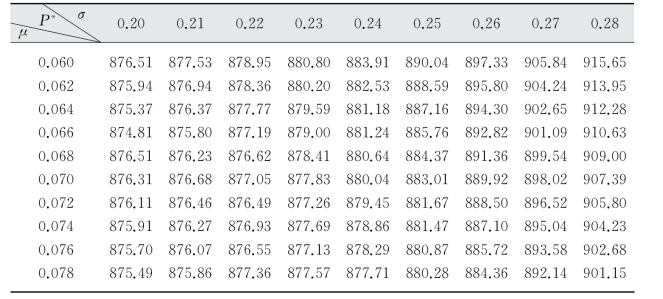
图5-2　r=0.04时P*取值与σ、μ的关系

（3）r=0.05。

表5-6　r=0.05时P*的取值

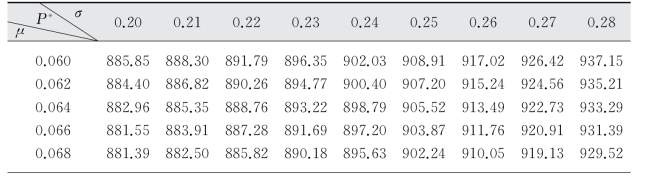
（续表）

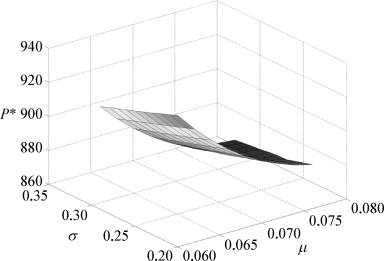
图5-3　r=0.05时P*取值与σ、μ的关系

由算例结果可知，当μ＞r时，执行价格P*总体上与σ和r呈正相关关系，而与μ则总体呈负相关关系。需要说明的是，图表中出现了个别不规则数据，这主要是由于非线性方程的解有可能不连续而造成的，并非错误结果。因此，从算例结果来看，本书所建立的模型针对认沽期权是有效的，符合期权理论的相关规律。

结合本书5.3.2节所述，简要说明该条件下班轮公司的决策方法。以表5-4为例，当r=0.03、μ=0.060、σ=0.20时，μ＞r，因而首先可确定所选择的期权决策类型应为认沽期权，表5-4中对应上述r、μ、σ值的执行价格P*值为861.86，即表明针对该附带认沽期权的运价协议，一旦市场价格波动至或超过861.86，班轮公司即应以该执行价格行使其认沽期权。换言之，当r=0.03时，若估值得到μ=0.060、σ=0.20，班轮公司在进行运输协议动态定价时，应决策选择附带认沽期权的运输协议，确定执行价格为861.86，执行时刻则是市场价格波动至该值或超过该值的实际时刻。

2）r取0.14、0.15、0.16(www.daowen.com)

r取0.14、0.15、0.16，即当μ＜r时相应的期权应为认购期权，此时P*与σ及μ为同方向变化关系，而与r为反方向变化关系，具体P*的取值及P*取值与σ、μ的关系如表5-7、表5-8、表5-9及图5-4、图5-5、图5-6所示。

（1）r=0.14。

表5-7　r=0.14时P*的取值

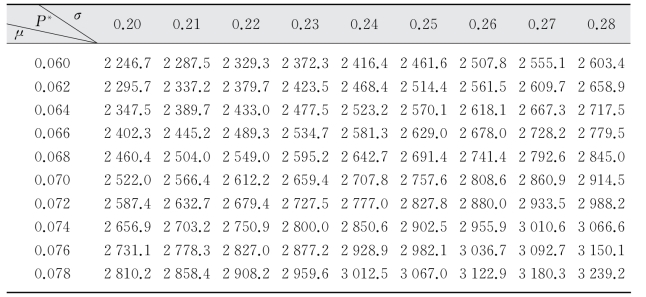
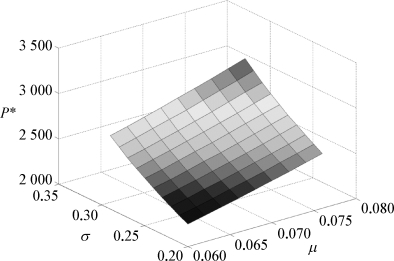
图5-4　r=0.14时P*取值与σ、μ的关系

（2）r=0.15。

表5-8　r=0.15时P*的取值

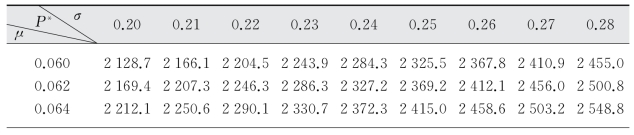
（续表）

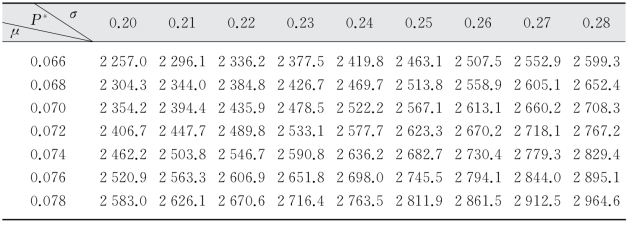
图5-5　r=0.15时P*取值与σ、μ的关系

（3）r=0.16。

表5-9　r=0.16时P*的取值

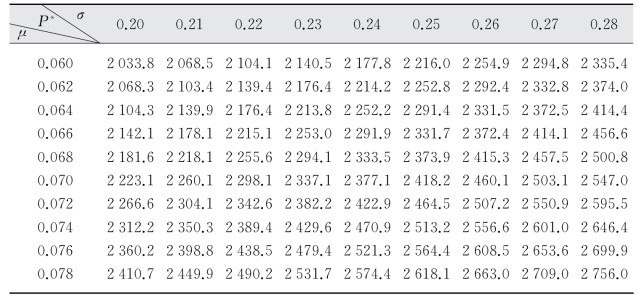
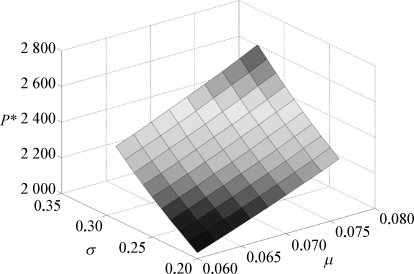
图5-6　r=0.16时P*取值与σ、μ的关系

由算例结果可知，当μ＜r时，执行价格P*总体上与σ和μ呈正相关关系，而与r则总体呈负相关关系。因此，由算例结果来看，本书所建立的模型针对认购期权也是有效的，符合期权理论的相关规律。

结合5.3.2节所述，简要说明该条件下班轮公司的决策方法。以表5-7为例，当r=0.14、μ=0.060、σ=0.20时，μ＜r，因而首先可确定所选择的期权决策类型应为认购期权，表5-7中对应上述r、μ、σ值的执行价格P*值为2 246.7，即表明针对该附带认购期权的运价协议，一旦市场价格波动至或低于2 246.7，班轮公司即应以该执行价格行使其认购期权。换言之，当r=0.14时，若估值得到μ=0.060、σ=0.20，班轮公司在进行运输协议动态定价时，应决策选择附带认购期权的运输协议，确定执行价格为2 246.7，执行时刻则是市场价格波动至该值或低于该值的实际时刻。

此外，从上述计算的定量结果也可以归纳出若干定性结论：总体上，期权标的瞬间报酬率标准差（波动率）的上升，会导致执行价格的上升；而期权标的的瞬间报酬率期望对执行价格的影响与期权的类型“一致”，即在认购期权时，报酬率期望的上升会导致执行价格上升，在认沽期权时，报酬率期望上升则会使得执行价格下降，这两点结论均符合“高风险，高收益”的基本准则。无风险折扣率对执行价格的影响与期权的类型“相反”，即在认购期权时，无风险折扣率的上升会使得执行价格下降，而在认沽期权时，无风险折扣率的上升则会使得执行价格上升，这也是符合期权投资理论的相关规律的。