本节通过算例分析来验证本书所研究的单分界点折扣方案的有效性，多分界点折扣方案也可采用类似方法实现。选用遗传算法进行求解。经过调试，最终设定染色体数为50，最大迭代数为40，染色体长度为20，选择概率为0.9。算法通过MATLAB编程实现，下文还将显示收敛过程。

为表述简洁，本节中利润单位为USD，箱位单位为TEU，运价和罚金率单位为USD·TEU-1，假设有20家NVOCC向班轮公司各自独立签订运价协议。第i家NVOCC面对的需求服从均匀分布D i～U（a i，b i）。通过推导式（4-19）和式（4-20）可以求得Q i0和Q i1，通过求解式（4-21），可以得到Q i01：

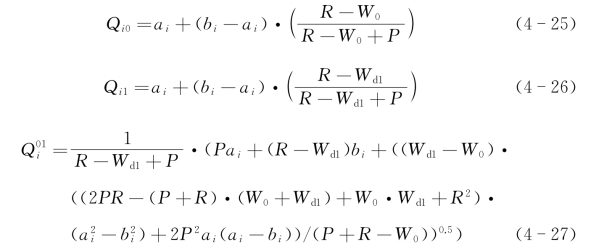
此外，假设班轮公司的单位运输成本为50，即C=50，标准运价为150，即W 0=150，基准罚金率为120，即P 0=120。NVOCC向真正托运人收取的运价为250，即R=250。所有a i均假设为0，根据不同的市场特征对b i进行假设。

1）NVOCC业务量等差分布

表4-10给出了体现NVOCC业务量等差分布的b i假设值。

表4-10　体现NVOCC业务量等差分布的bi假设值

在无数量折扣的销售方案下，所有NVOCC的订舱总量为52 727，所有NVOCC的总利润为2 636 364，班轮公司的总利润为5 512 397。

在包含罚金条件的单折扣点方案下，图4-8表示了班轮公司总利润与折扣运价之间的关系，表明过低或过高的折扣运价对于班轮公司的总利润均有负面影响。

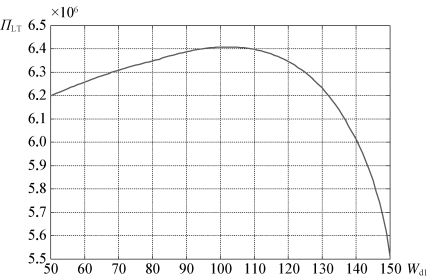
图4-8　NVOCC业务量等差分布假设下班轮公司采用不同折扣运价时的总利润

在该条件下，班轮公司的最优折扣点为8 366，相应的折扣运价为102.16。所有NVOCC的订舱总量为71 148，较52 727高出34.94%，所有NVOCC总利润为3 068 756，较2 636 364高出16.40%，班轮公司从所有NVOCC处获得的利润为6 407 333，较5 512 397高出16.23%。

如果将罚金率P也作为一个决策变量，那么W d1、P和ΠLT之间的关系将更为复杂，图4-9表示了班轮公司总利润与不同折扣运价及罚金率组合之间的关系。

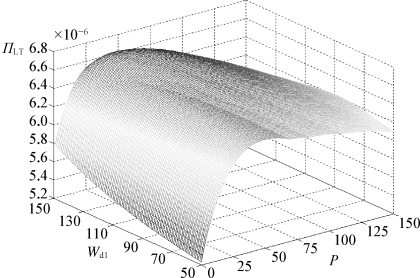
图4-9　NVOCC业务量等差分布假设下班轮公司总利润与不同折扣运价和罚金率组合之间的关系

此条件下，最优罚金率P*为52.41，班轮公司的最优折扣点为9 623，相应的折扣运价为132.79。如表4-11所示，所有NVOCC的订舱总量为86 784，较71 148高出21.98%，所有NVOCC总利润为3 950 417，较3 068 756高出28.73%，班轮公司从所有NVOCC处获得的利润为6 729 136，较6 407 333高出5.02%。

表4-11　NVOCC业务量等差分布假设下不同情况下NVOCC最优订舱量和利润及班轮公司利润

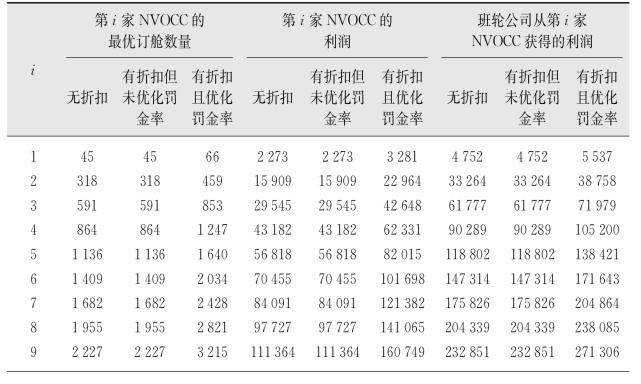
（续表）

图4-10（a）和（b）分别显示了罚金率未优化和优化时遗传算法的迭代过程。可以发现，迭代到第15～25代之间，即可取得最优解。表4-11给出了不同情况下，每一家NVOCC的最优订舱数量和利润，以及班轮公司从每一家NVOCC获得的利润。

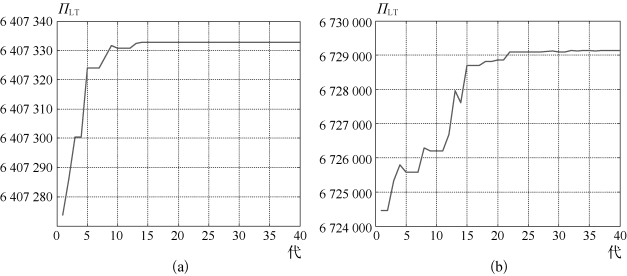
图4-10　NVOCC业务量等差分布假设下班轮公司总利润收敛过程

（a）未对罚金率进行优化；（b）对罚金率进行了优化(www.daowen.com)

不论是否对罚金率进行优化，在各数量折扣方案下，所有NVOCC的利润都不会下降，表明折扣方案对于班轮公司和NVOCC是双赢的策略。若不对罚金率进行优化，第1～15家NVOCC属于第1类，第16～20家NVOCC属于第2类；若对罚金率进行优化，第1～16家NVOCC属于第1类，第17～20家NVOCC属于第2类。两种情况下，均没有NVOCC属于第3类。

2）多数NVOCC业务量处于中间水平

表4-12给出了体现多数NVOCC业务量处于中间水平的b i假设值，这也更接近现实市场情况。在这样的市场下，大NVOCC和小NVOCC数量均相对较小，中等规模NVOCC构成班轮公司所面对的市场主体。

表4-12　体现多数NVOCC业务量处于中间水平的b i假设值

在无数量折扣的销售方案下，所有NVOCC的订舱总量为52 000，所有NVOCC的总利润为2 600 000，班轮公司的总利润为5 436 364。

在包含罚金条件的单折扣点方案下，图4-11显示了班轮公司总利润与折扣运价之间的关系，同样表明过低或过高的折扣运价对于班轮公司的总利润均有负面影响。

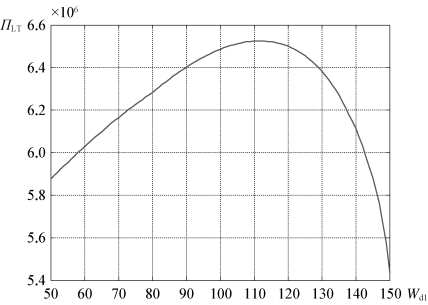
图4-11　市场主体为中等规模NVOCC假设下班轮公司采用不同折扣运价时的总利润

在该条件下，班轮公司的最优折扣点为4 949，相应的折扣运价为111.67。所有NVOCC的订舱总量为76 041，较52 000高出46.23%，所有NVOCC总利润为3 386 166，较2 600 000高出30.24%，班轮公司从所有NVOCC处获得的利润为6 525 202，较5 436 364高出20.03%。

如果将罚金率P作为一个决策变量，那么W d1、P和ΠLT之间的关系将更为复杂，图4-12表示了班轮公司总利润与不同折扣运价及罚金率组合之间的关系。

图4-12　市场主体为中等规模NVOCC假设下班轮公司总利润与不同折扣运价和罚金率组合之间的关系

此条件下，最优罚金率P*为61.36，班轮公司的最优折扣点为5 581，相应的折扣运价为134.38。如表4-13所示，所有NVOCC的订舱总量为85 112，较76 041高出11.93%，所有NVOCC总利润为3 874 821，较3 386 166高出14.43%，班轮公司从所有NVOCC处获得的利润为6 655 595，较6 525 202高出2.00%。

表4-13　市场主体为中等规模NVOCC假设下不同情况下NVOCC最优订舱量和利润及班轮公司利润

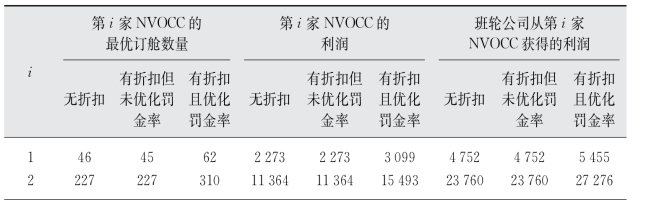
（续表）

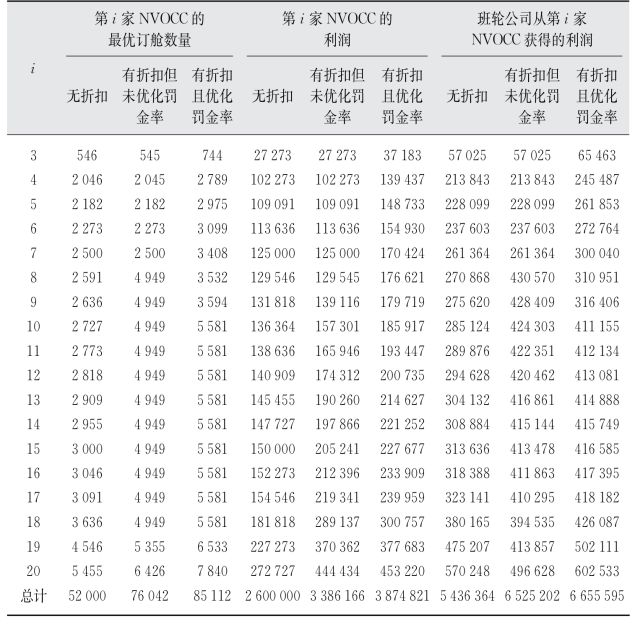
图4-13（a）和（b）分别显示了罚金率未优化和优化时遗传算法的迭代过程。可以发现，迭代到第15～25代之间，即可取得最优解。表4-13还给出了不同情况下，每一家NVOCC的最优订舱数量和利润，以及班轮公司从每一家NVOCC获得的利润。

不论是否对罚金率进行优化，在各数量折扣方案下，所有NVOCC的利润都不会下降，表明在该假设下，折扣方案对于班轮公司和NVOCC也是双赢的策略。若不对罚金率进行优化，第1～7家NVOCC属于第1类，第8～18家NVOCC属于第2类，第19～20家NVOCC属于第3类；若对罚金率进行优化，第1～9家NVOCC属于第1类，第10～18家NVOCC属于第2类，第19～20家NVOCC属于第3类。

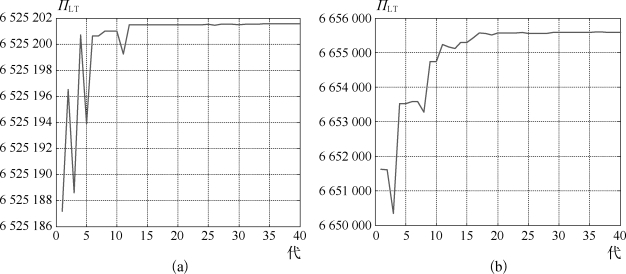
图4-13　市场主体为中等规模NVOCC假设下班轮公司总利润收敛过程

（a）未对罚金率进行优化；（b）对罚金率进行了优化

基于算例分析可以发现：优化的数量折扣方案可以给班轮公司带来更为丰厚的利润；当罚金率也作为一个决策变量来进行优化时，班轮公司的利润可以得到进一步提升；无论是否对罚金率进行优化，没有一家NVOCC的收益会降低；在算例所反映的两种典型情况下，若不对罚金率进行优化，并非所有NVOCC的利润都会得到提高；对于班轮公司而言，数量折扣对其提高利润较之优化罚金率更为有效，而对于NVOCC而言，优化罚金率对提升他们利润的影响更广泛、更明显。