多分界点数量折扣方案能够给班轮公司带来更丰厚的利润，理想的价格函数应该是为每一个不同的订舱数量Qi设定不同的W（Q i）。为了获取比单折扣点更高的利润，设定多个折扣点是一个可行的方案。若设定r个折扣点，数量折扣方案可以表达为

若第i家NVOCC可使用折扣运价W d u（u=0，…，r），利润可表达为

同样基于报童模型理论，通过式（4-24）可求取使得ΠF i（Q i，W d u）达到最大值的Qiu：

类似地，第i家NVOCC的最优订舱数量备选方案包括Q iα（α=0，…，r），以及Q dβ（β=1，…，r）。决策流程如下：

第1步：计算Q iα（α=0，…，r），备选方案集合为Ω={Qiα，α=0，…，r}∪{Q dβ，β=1，…，r}。

第2步：如果Qiβ＜Q dβ，从Ω中去除Q iβ，否则，从Ω中去除Q dβ。

第3步：在Ω中仅保留maxβ{Qiβ}，去除其他所有Qiβ。

第4步：选择使得ΠF i取得最大值的Qi∈Ω。

基于订舱数量，所有的NVOCC可以分为以下2r+1组，即其订舱量分别为Q i0，Q d1，Qi1，…，Q d r，Qir。属于第2，4，…，2r组的NVOCC会受数量折扣方案诱导，从而提高其订舱数量。问题至此可以描述为，找到方案S（Q*d1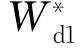， ；…；Q*d r，W*d r；P*），使得班轮公司的总利润最大。

令Qitu为大于Qiu的Qi值，且满足ΠF i（Q i，W d u，P）=ΠF i（max（Qit，Q d t），W d t，P）（0≤t＜u），以下性质可以减小Q d u的解空间。(www.daowen.com)

性质3：给定W d u（u=1，…，r，W 0＞W d1＞W d2＞…＞W d r＞C）和P的组合，存在一个可取得ΠLT最大值的Q d u（0＜Q d1＜Q d2＜…＜Q d r）集合，满足Q d u=Qitu（i∈N，u=1，…，r，t=0，…，（u-1））或取大于i m，t a，x u Qitu的任意值。

证明：假设给定Q d l（l＜u），搜索特定u值下的Q d u解空间。对于所有Qits[i∈N，s=1，…，（u-1）且t=0，…，（s-1）]，将按照升序排列Qits，并令序号依次为V 1，V 2，…，V q，并令V 0=0。Q d u在（0，+∞）区间上可以用V i分为q+1个区段。令Q d u处于第j个区段内（j为1到q之间的任意数值），即V j-1＜Q d u≤V j。假设Q d u从V j-1+ε变化至V j（ε为无穷小的正值），NVOCC便可据此分为两组：第1组NVOCC的最优订舱数量，当Q d u=V j-1+ε时，为Q d u，甚至当Q d u=V j时，仍为Q d u；第2组NVOCC的最优订舱数量，当Q d u=V j-1+ε时，为Qiu，当Q d u位于区段中某一点时，则变为Q d u，直到Q d u取值至V j。需要注意的是，对于两组NOVCC而言，W d u均是适用的，且因此，在Q d u处于第j个区段的假设下，当Q d u=V j时，班轮公司的利润最大。如果Q d u的最优值位于区段（V q，+∞）中，则意味着相应的折扣价格太低，以至于班轮公司不希望有任何一家NVOCC能够利用这第u个折扣价格。

证毕。

假设相邻折扣点之间的间隔足够远，每一家NVOCC无需考虑多个折扣点即可确定其订舱数量，可称之为“每家NOVCC仅考虑单个折扣点假设”。

假设Qit=max（Qis|Q is≤Q d s），那么，若ΠF i（Q it，W d t，P）＞ΠF i（Q d（t+1），W d（t+1），P），则第i家NVOCC的订舱数量为Q it，否则，为Q d（t+1）。也就是说，第i家NVOCC无需考虑Q d（t+2），…，Q d r，因为它们太大了，不会成为其经济订舱量。这个假设也是合理的，因为不同的折扣点用于吸引不同组别的NVOCC，他们相应具有不同订舱数量需求。令Q（u-1）ui取大于Qiu的Qi值，且满足ΠF i（Qi，W d u，P）=ΠF i（Q i（u-1），W d（u-1），P），那么可得以下推论。

推论：在“每家NVOCC仅考虑单个折扣点假设”下，给定W d u（u=1，…，r，W 0＞W d1＞W d2＞…＞W d r＞C）和P组合，存在一组折扣点Q d u（0＜Q d1＜Q d2＜…＜Q d r），可使得班轮公司ΠLT总利润最大，其中Q d u取值为Qi（u-1）u（ i∈N，u=1，…，r）或任意大于m i a，u x Qi（u-1）u 的值。

证明：从Q d u的备选值中去除除Q（u-1）ui之外的所有Q tui，结论成立。证毕。

性质3及其推论对于多分界点折扣方案下减小折扣点搜索空间非常有帮助。与前节所讨论的单分界点问题一样，本节的多分界点问题也用遗传算法或其他适合的搜索算法实现求解。