与前节相似,本节同样假设班轮公司与NVOCC之间就一段时间内的箱位销售达成包含数量折扣条件的协议,NVOCC承诺的舱位订购量越高,其享受的数量折扣条件越优厚,但若NVOCC未能完成其在签约时所承诺的订舱量,则他需向班轮公司支付一定的罚金。
本节涉及的变量及其含义如下:
1)NVOCC角度的输入变量
N:n家NVOCC序号的集合,{1,2,…,n};
R:NVOCC将箱位销售给托运人的运价;
D i:第i家NVOCC面对的运力需求;
f i(·):第i家NVOCC运力需求的概率密度函数;
F i(·):第i家NVOCC运力需求的累积分布函数;
F-1i(·):第i家NVOCC运力需求的累积分布函数的反函数。
2)班轮公司角度的输入变量
C:班轮公司的单位运输成本,包括固定成本与变动成本;
W 0:班轮公司提供给NVOCC的基准运价;
P 0:班轮公司针对未能提供约定箱量的NVOCC的基准罚金率(与前节定金原理相似)。
3)决策变量
Q i:班轮公司与第i家NVOCC约定的订舱量;
W(·):班轮公司在运价协议中提供给NVOCC的折扣运价,是订舱量的函数,取值范围为(C,W 0);
P:班轮公司针对未能提供约定箱量的NVOCC的折扣罚金率。
4)利润函数
ΠF i:第i家NVOCC的期望利润,也可表示为ΠF i(Qi,W(Q i),P);
ΠL i:班轮公司从第i家NVOCC处获得的期望利润,也可表示为ΠL i(Qi,W(Qi),P);
ΠLT:班轮公司从所有NVOCC处获得的总期望利润,也可表示为ΠLT(W(·),P)。
第i家NVOCC的期望利润可以表达为
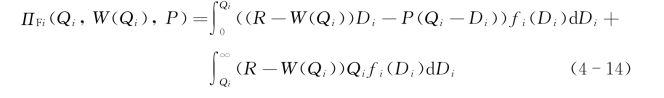
班轮公司从第i家NVOCC获得的期望利润可以表达为
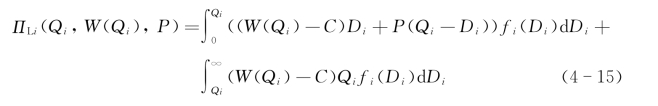
班轮公司从所有NVOCC获得的总期望利润可以表达为
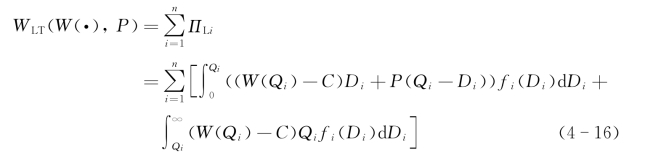
班轮公司的数量折扣方案可表达为
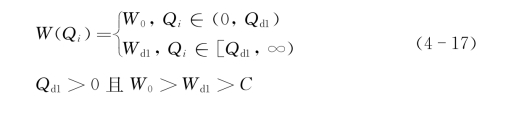
式中,Q d1与W d1为数量折扣分界点及其对应的折扣价格。
性质1:对于式(4-17)所给出的单分界点数量折扣方案,第i家NVOCC最优订舱数量Q i可以由下式决定:

其中,
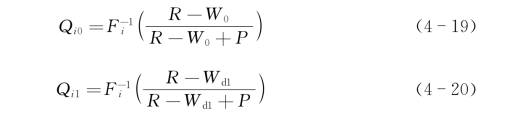
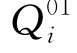 满足式(4-21)且大于Qi1的Qi值:
满足式(4-21)且大于Qi1的Qi值:
![]()
证明:若第i家NVOCC使用基准运价,则其利润可表达为
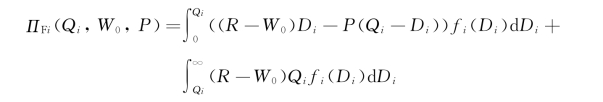 (https://www.daowen.com)
(https://www.daowen.com)
可得ΠF i(Qi,W 0,P)对Qi的一阶导数:
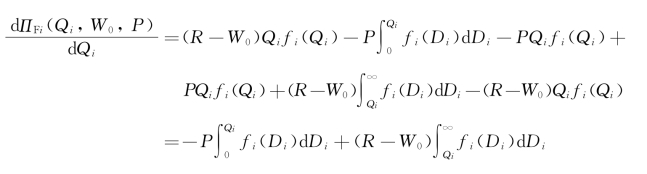
二阶导数:
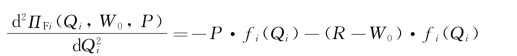
因为P>0,R>W 0,且f i(Qi)>0,![]() ,因此,ΠF i(Q i,W 0,P)是凹函数。为求得可使ΠF i(Q i,W 0,P)取最大值的Q i0值,令
,因此,ΠF i(Q i,W 0,P)是凹函数。为求得可使ΠF i(Q i,W 0,P)取最大值的Q i0值,令![]() ,即
,即![]() 0。由
0。由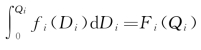 及
及![]() 可得F i(Q i)=
可得F i(Q i)=![]() ,因此式(4-19)成立。
,因此式(4-19)成立。
当第i家NVOCC可使用折扣运价,其利润可表达为
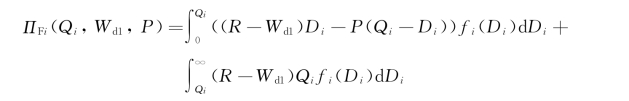
为求取可获得最大收益ΠF i(Q i,W d1,P)的Qi1,令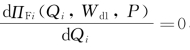 ,即可得到式(4-20)。
,即可得到式(4-20)。
由W d1<W 0可知Q i0<Qi1。由ΠF i(Qi,W d1,P)>ΠF i(Qi,W 0,P)及Qi 0<Qi10可知,第i家NVOCC的利润函数如图4-6所示。因此,取决于Q d1的不同位置,将有三种情形,即①Q i01≤Q d1,②Q i1<Q d1<Q i01及③Q d1≤Q i1,如图4-7所示。
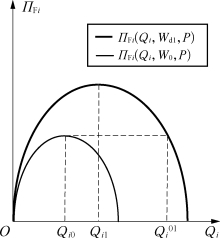
图4-6 NVOCC在各定金比率下的最优协议箱量与相应收益曲线
证毕。
从班轮公司的角度来看,NVOCC可以根据式(4-18)分为三类:属于第2类的NVOCC会受折扣方案的诱导,选择提升他们的订舱至Q d1;第1类NVOCC属于“小”公司,订舱量远小于折扣点;第3类NVOCC则属于“大”公司,可以搭便车享受折扣优惠。
性质2:对于给定的折扣费率W d1和罚金率P,当Q d1取值为Q i01或任意大于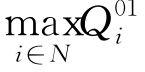 的值时(i∈N),ΠLT取得最大值。
的值时(i∈N),ΠLT取得最大值。
证明:为简明表达,将所有NVOCC按照他们的约定订舱量Q i01升序排列,即Q 011≤Q 021≤…≤Q n01-1≤Q n01,令Q 001=0。整个Q值区间可以分为(Q 001,Q 011],(Q 011,Q 021],…,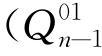 ,Q n01],(Q n01,+∞)。再次用到
,Q n01],(Q n01,+∞)。再次用到
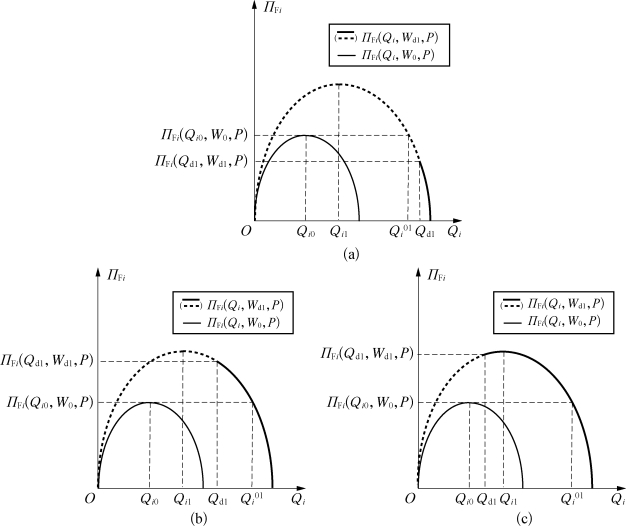
图4-7 NVOCC在各定金比率下的最优协议箱量与相应收益曲线
(a)Qi01≤Q d1;(b)Qi 1<Q d1<Qi01;(c)Q d1≤Qi1
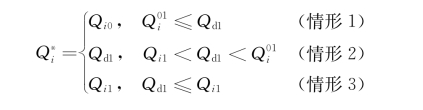
(1)若Q d1∈(Q 01k-1,Q 01k],k∈N:
若i≤k,即Q 01i≤Q d1,Qi=Q i0,班轮公司的相应利润为ΠL i(Q i0,W 0,P)。
若k<i≤n,即Q 01i>Q d1,Qi=max(Qi1,Q d1),班轮公司从第i家NOVCC赚取的利润为ΠL i(max(Qi1,Q d1),W d1,P)。考虑到![]()
![]() 因此,对于给定的W d1,ΠL i(Q i,W d1,P)随Q i单调递增。所以,当Q d1∈(Q 01k-1,Q 01k],班轮公司应将Q d1设为Q 01k以获取最大利润。
因此,对于给定的W d1,ΠL i(Q i,W d1,P)随Q i单调递增。所以,当Q d1∈(Q 01k-1,Q 01k],班轮公司应将Q d1设为Q 01k以获取最大利润。
(2)若Q d1∈(Q 01n,+∞):
Q 01i<Q d1,因而对于全体i,Qi=Qi0,换言之,如果Q d1在该区间,即相当于没有采用折扣方案。相应地,班轮公司从第i家NOVCC赚取的利润为ΠL i(Q i0,W 0,P)。
综上所述,对于给定的折扣费率W d1,当Q d1取值为Q 01i(i∈N)或任意大于![]() 的值时,班轮公司可得最大总利润ΠLT。
的值时,班轮公司可得最大总利润ΠLT。
证毕。
根据性质2,若给定W d1和P组合,通过搜索有限的备选值即可获得最优Q d1的方法。接下来探讨如何求取最优W d1和P的方法,如遗传算法(genetic algorithm,GA)、蚁群优化算法(ant colony optimization,ACO)、粒子群算法(particle swarm optimization,PSO)等算法均可用于搜索可令班轮公司赚取最大利润ΠLT的W d1和P组合(W d1∈(C,W 0),P∈[0,W 0])。
本书选用遗传算法求解,以下简要说明相应的编码、解码、交叉、变异、适应度评估、选择等步骤。基于MATLAB的遗传算法工具箱实现求解。
第1步:生成W d1和P的初始种群,令gen=1。
第2步:在当前种群下为每个染色体解码。
第2.1步:计算所有n家NVOCC的Qi0、Qi1和Q 01i值。
第2.2步:计算所有Q d1=Qi01时的ΠLT值,令其中最大的ΠLT值为ΠLT。
第3步:gen=gen+1。如果gen值超过设定的最大代数,则转至第4步;否则,生成下一代的种群。
第3.1步:(选择)按照一个预先设定的百分比(通常也称为“代沟”)从前代群体中选取具有最佳适应度的染色体,去除其余染色体。
第3.2步:(交叉)随机但按一定百分比,对第3.1步所选择的染色体使用交叉算子。
第3.3步:(变异)随机但按一定百分比,对第3.2步所获得的染色体使用变异算子。
第3.4步:按照一定百分比,从第3.3步所获得的染色体中选择具有最佳适应度的后代染色体;用新选取的染色体替换前代群体中最差的染色体;转至第2步。
第4步:比较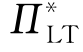 和
和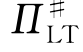 (班轮公司不采用数量折扣时的利润),选择能够获取最高利润的方案,即班轮公司的最大利润,输出相应的数量折扣方案。
(班轮公司不采用数量折扣时的利润),选择能够获取最高利润的方案,即班轮公司的最大利润,输出相应的数量折扣方案。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







