考虑诸多现实因素并全面改进经典报童模型之后，直接求出该模型的解析解已经变得相当困难，而采用数值仿真的方法，则可相对容易地直接求出典型算例的数值解并找出该类问题的核心影响因素及其相应的变化规律，并可将总结出的相关规律作为班轮公司与NVOCC协议决策的重要科学依据。

本节将通过考察定金比率、折扣区间、折扣比率等核心决策要素，确定双方的主要决策依据。为表述简洁，箱量单位为TEU，收益单位为USD，价格单位为USD·TEU-1。

受计算机运算速度所限，在利用MATLAB编写程序进行数值仿真时，将相关数值做一定比例的缩小。

1）变动定金比率对NVOCC协议箱量及班轮公司收益的影响

假设NVOCC的箱位销量服从参数λ=950的泊松分布，其售出价格为1 000。班轮公司出售舱位的基准价格为800，折扣区间及相应折扣比率如表4-1所示。

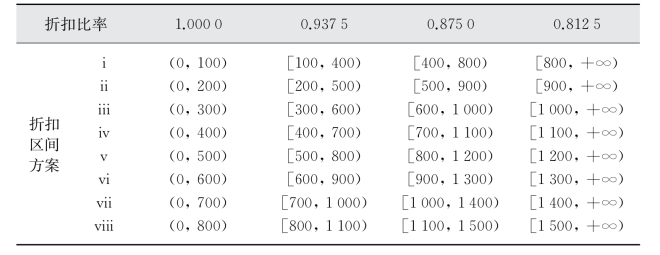
表4-1　折扣区间及相应折扣比率

设定定金比率α分别为0.15、0.20、0.25、0.30、0.35、0.40、0.45及0.50，仿真得到的NVOCC最优协议箱量、相应收益及收益曲线走势如表4-2和图4-1所示。

表4-2　NVOCC在各定金比率下的最优协议箱量与相应收益

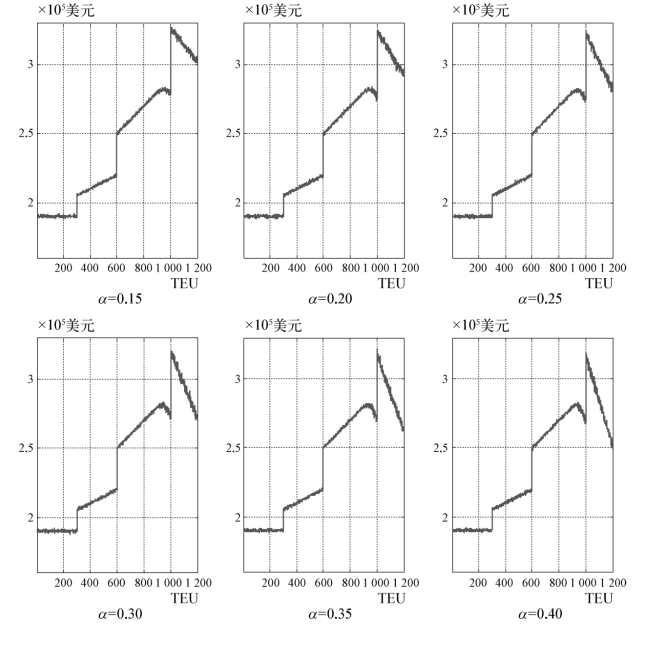
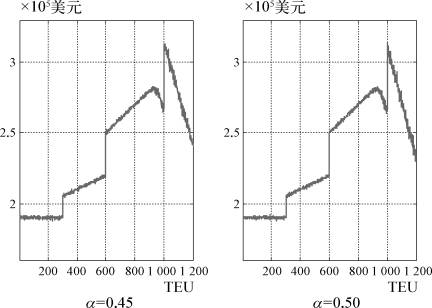
图4-1　NVOCC在各定金比率下的最优协议箱量与相应收益曲线

由表4-2与图4-1可以发现，定金比率从0.15～0.50的变动，对NVOCC最优协议箱量及相应最大收益的实际影响并不大，基本都在1 000（最优惠折扣区间的下限）附近，相应的最优收益变化也不大。从图4-1中更可直观地发现，NVOCC的协议箱量在各定金比率下，收益曲线形态也非常相似，在几个折扣区间分界点的变动均非常显著。当然，从曲线形态的变化趋势来看，随着定金比率的进一步提升，其形态将会产生进一步变化，即收益峰值会转移至次优惠折扣区间，但在实际业务中，定金比率通常不会超过0.50，因而本章不再考察α＞0.50的情况。

基于表4-2可以计算出如表4-3所示的班轮公司在不同定金比率下的协议箱量及其对应收益值，并可确定在给出的8个定金比率方案下，定金比率取0.20时，班轮公司获得其最优收益655 850。但同时不难发现，不同的定金比率方案对班轮公司最优收益的实际影响并不大。因此，定金比率实际上并非本章假设背景下数量折扣决策的关键要素。

表4-3　班轮公司在各定金比率下的协议箱量与对应收益

2）变动折扣区间对NVOCC协议箱量及班轮公司收益的影响

假设NVOCC舱位销量服从参数λ=950的泊松分布，其售出价格均为1 000。班轮公司出售舱位的基准价格为800，设定的定金比率为0.20，并设定表4-4中的8种折扣区间方案。

表4-4　折扣区间方案

经数值仿真，得到的NVOCC最优协议箱量、相应收益及收益曲线走势如表4-5和图4-2所示。

表4-5　NVOCC在各折扣区间方案下的最优协议箱量与相应收益

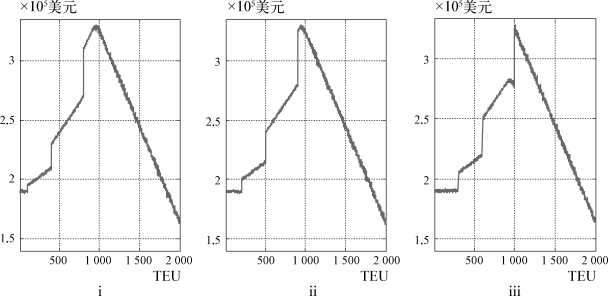
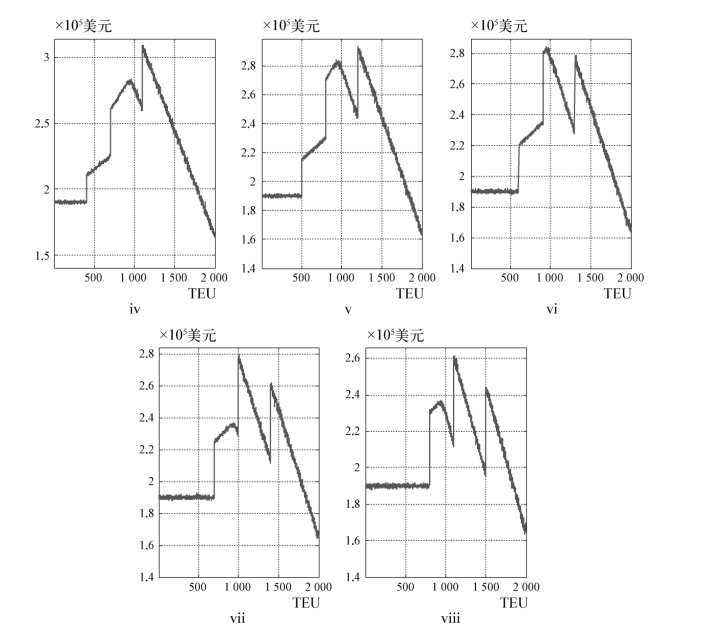
图4-2　NVOCC在各折扣区间方案下的最优协议箱量与相应收益曲线(www.daowen.com)

通过表4-5与图4-2可以发现，在不同的折扣区间方案下，NVOCC的最优协议箱量所对应的最大收益呈明显的递减趋势。同时，随着折扣区间各分界点与λ大小关系的逐步变化，最优协议箱量点的数值分布也表现不同特点。方案i与方案ii下，最优惠折扣区间的下限不超过λ值，则最优协议箱量的数值比较接近该值，分别为961、934，而且在方案i下，最优协议箱量值是渐进到达的，不像其他7个方案下，几乎均为跃升到达。从方案iii开始，最优惠折扣区间的下限超过λ值，最优协议箱量开始逐步向相应的次优惠折扣区间下限值转移，而且随着次优惠折扣区间下限值的逐步上升，最优协议箱量也越来越接近相应的次优惠折扣区间的下限，收益曲线也由单峰向多峰形态转变。不难推断，随着次优惠折扣区间下限的逐步上升，NVOCC的最优协议箱量将进一步向下一折扣优惠区间转移。

由此可知，单纯的数量折扣区间变动对NVOCC最优协议箱量的影响是有限的，而随着NVOCC销售需求分布的参数值λ与各数量折扣优惠区间下限大小关系的逐步变化，其最优协议箱量的变动则会产生更为丰富的规律性变化。因此，班轮公司在进行折扣区间设计时，对于NVOCC舱位销售需求分布及相关参数的掌握相当重要，也是其科学决策必不可少的，盲目地变动折扣区间并不一定能够达到其预期的诱导效果。

基于表4-5可以计算出如表4-6所示的班轮公司在不同折扣区间方案下的协议箱量与对应收益值，并可确定在8个折扣区间方案下，选择实施方案v时，班轮公司可以获得其最优收益780 650 USD。对比定金比率对班轮公司收益的影响，可以发现不同折扣区间的设置会对班轮公司的最优收益产生较大的影响。班轮公司在方案v下所取得的最优收益780 650 USD要比方案ii下取得的最劣收益615 550 USD高出26.82%。

表4-6　班轮公司在各折扣区间方案下的协议箱量与对应收益

3）变动折扣比率对NVOCC协议箱量及班轮公司收益的影响

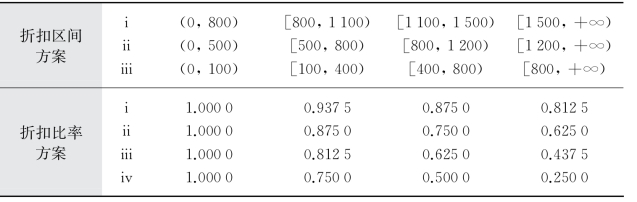
假设NVOCC销量服从参数λ=950的泊松分布，其售出价格均为1 000。班轮公司设定的定金比率为0.20，无折扣优惠的基准价格均为800。考察（0，800）、[800，1 100）、[1 100，1 500）、[1 500，+∞），（0，500）、[500，800）、[800，1 200）、[1 200，+∞），（0，100）、[100，400）、[400，800）、[800，+∞）等三个典型折扣区间方案下，折扣比率变动对NVOCC最优协议箱量的影响。具体各区间的折扣比率方案如表4-7所示。

表4-7　各区间的价格折扣方案

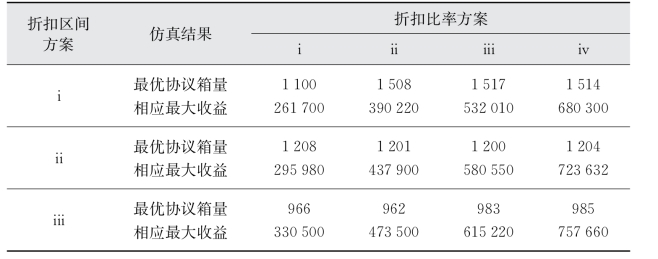
经数值仿真，得到的NVOCC在不同区间与价格折扣方案组合下的最优协议箱量与相应的收益如表4-8所示。

表4-8　NVOCC在各区间方案及折扣比率方案下的最优协议箱量与相应收益

三个折扣区间方案下，各折扣比率方案下的NVOCC最优协议箱量与相应的收益曲线走势如图4-3、图4-4、图4-5所示。

通过表4-8及图4-3、图4-4、图4-5可以发现，在给出的各典型折扣区间方案下，随着折扣力度的加大，NVOCC的最大收益均有明显提高，但其最优协议箱量的上升却不明显，这基本符合本节第2小节总结的相关规律，而曲线形态的变化也基本符合本节第2小节总结的相关规律。

基于表4-8，可以计算出如表4-9所示的班轮公司在各区间方案及折扣比率方案下的协议箱量与对应收益。

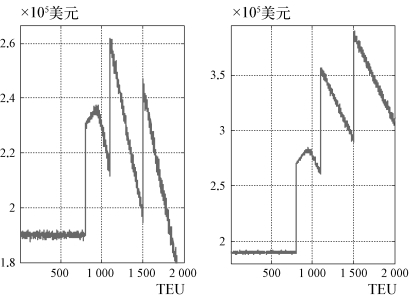
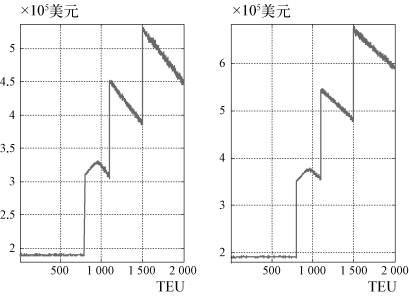
图4-3　区间方案i下，各折扣比率方案下的NVOCC协议箱量与相应收益曲线

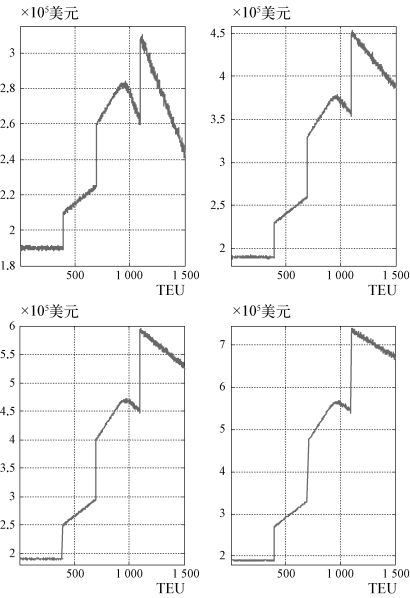
图4-4　区间方案ii下，各折扣比率方案下的NVOCC协议箱量与相应收益曲线

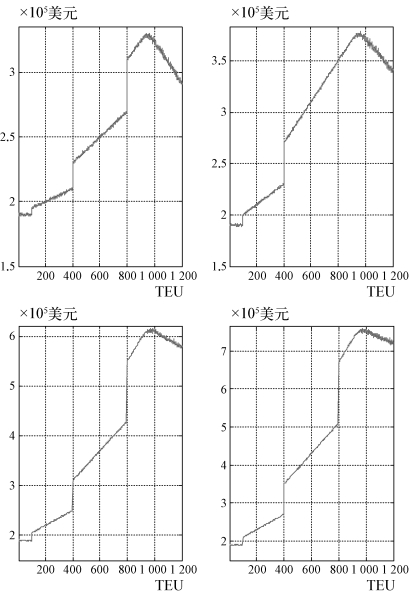
图4-5　区间方案iii下，各折扣比率方案下的NVOCC协议箱量与相应收益曲线

表4-9　班轮公司在各区间方案及折扣比率方案下的协议箱量与对应收益

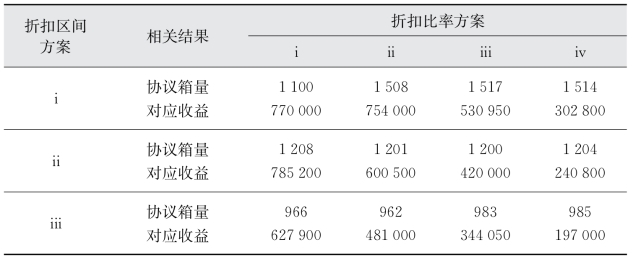
可以进一步发现，在各典型折扣区间下，如果班轮公司只是单纯地加大折扣，NVOCC的期望收益会得到显著提高，但班轮公司的舱位销量变化并不大。而且，班轮公司自身收益也呈现出逐渐恶化的趋势。

通过本节所进行数值仿真可知，定金比率的变动，对NVOCC最优协议箱量及相应最大收益的实际影响甚微；忽视NVOCC销售需求分布的参数值λ，单纯的数量折扣区间变动对NVOCC最优协议箱量的影响也是非常有限的，若想通过变动折扣区间改善收益，必须紧密结合NVOCC销售需求分布的具体情况，而且，折扣区间的设置对班轮公司的最优收益有较大的影响。

结合企业经营的具体数据，班轮公司可以基于以上结论，合理综合多方面的决策因素，以确定对其收益最为有利的数量折扣方案。