假设协议运价不是常数，而是可以在公布运价p的基础上，享受与订舱折扣区间下限Q=（q 1，q 2，…，q j，…，q n）T相关的n个等级的折扣，相应的折扣比率为Θ=（θ1，θ2，…，θj，…，θn）T，1≥θ1＞θ2…＞θj＞…＞θn＞0，对应不同协议箱量q的协议运价P=（p 1，p 2，…，p j，…，p n）T。向量P中的元素p j由函数P（q）确定，即

相应地，该条件下k与h也应为与q相关的函数，不妨表示为k（q）与h（q），则k（q）=z-P（q），h（q）=αP（q），且z＞θ1p。当箱位供不应求时（s＞q），NVOCC的收益为k（q）·q；当箱位供过于求时（s＜q），相应的收益为k（q）sh（q）·（q-s）。故此条件下NVOCC的收益期望可表示为

同理，若q*j为某数量折扣区间的最优订舱量，当q*j-1、q*j、q*j+1属于同一折扣区间时，通过边际分析应有

或

确定最优协议箱量q*可归纳为以下三个步骤。(www.daowen.com)

（1）在不同的区间[q j，q j+1）下，将P（q）=θjp代入式（4-7）或式（4-8），分别求出n个等级折扣区间下的。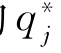

（2）对于求解得到的所有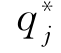，若∈[q j，q j+1），则不做任何变化，若q*j＜q j，则令q*j=q j，若q*j＞q j+1，则令q*j=q j+1-1，分别求出q*1，q*2，…，q*j，…，q*n。

（3）