本章第3节建立的优化模型可进一步推广到更为复杂的供需函数下进行应用。

恒弹性价格反应函数在反映局部情况时，是相对有效的工具，但若作为描述顾客行为的一般性模型，它们不可避免地存在着较为严重的局限性。正因如此，本章第5节的试验4与试验5也尝试做了较为复杂的变化，为模型的进一步推广奠定了相应的基础。

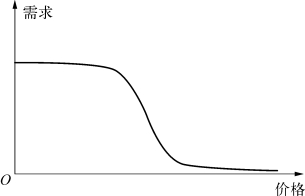
图3-4　反S形价格反应曲线

通常情况下，顾客行为可能会与如图3-4所示的反S形反应曲线较为吻合，即当定价较低时，会得到很多需求，定价较高时，只能得到很少的需求，但在这两段区间，需求变化相对于价格变化均不是非常敏感。在中间区域，需求对价格会变得非常敏感，价格的微小变化可以引起需求的巨大反应。

研究表明，这种一般形式的价格反应曲线适用于绝大多数的价格反应行为，而最常用到的反应函数即为Logit价格反应函数，即

式中，a、b、C为参数，且b、C＞0，a的符号不限，但通常定义a＞0。广义上说，C表示某种商品的整体市场规模，b表示价格敏感程度，其值越大，相应的价格敏感性越强，在点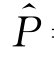=a/b上，价格敏感性曲线最陡峭，该点在经济学理论中通常近似地认为是“市场价格”。(www.daowen.com)

由该函数的基本数学性质可知，此时ΔP与ΔQ之间近似存在以下关系：

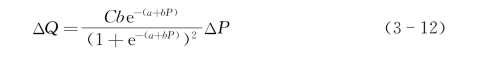
因此，本章第3节的优化模型式（3-4）可相应变化为

通过比较可以发现，经推广后的模型的目标函数实际上与之前模型一样，只是约束条件的表达式产生一定的变化，主要体现在两个方面：①原约束条件2，即ΔP i与ΔQ i的映射关系比原模型表达的更为具体；②考虑到Logit函数表达中的C已体现了整体的市场规模，因此原优化模型中的约束条件4即可略去。

因为参数a i、b i、C i值以及初始P值在特定条件下均可通过数据直接获得或求取获得。因此，在上述Logit价格反应函数下ΔP i与ΔQ i的映射关系实际上也可近似线性表达，即本章第3节对不同k i值变化规律下优化结果的分析结论也是适用的。

由此可知，若将本章第3节建立的模型进行进一步推广，在更为复杂的价格-需求关系下，所建立的优化模型仍可以发挥相应优化效果。