本节选取某班轮公司在某港口的某个具有代表性的航次上接受托运的集装箱数量与重量数据作为具体算例，详细阐述模型的求解与应用。为表述简洁，本节中，箱量及箱位单位为TEU，集装箱重量及船舶载重吨单位为t，收益单位为USD，运价单位为USD·TEU-1。

1）数据基本分析与折扣区间确定

首先对数据进行基础性的统计分析。将样本集装箱的重量折算为每TEU重量导入SPSS进行统计学特征的基础性分析。所得主要参数的描述性结果及直方图如表3-2及图3-1所示。样本集装箱折合标准箱数为7 684，重量均值为14.551 4 t，重量方差为6.406 22，即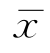=14.551 4，s=6.406 22。

表3-2　SPSS计算结果（1）

该班轮公司选用了一艘载箱量约为8 000、净载重吨约为80 000 t的全集装箱船舶执行该航次的运输任务。从所抽取样本的TEU箱重均值来看，该值已明显超出船舶的TEU平摊载重吨。因此可以说，所抽取样本中的“偏重箱”过多，即该重量分布的箱源必将导致船舶在载运过程中满载不满舱。若近似采取按照重量从大至小的原则从样本集装箱中选择拒载，则为了满足船舶的载重吨限制，最终承运的集装箱最多仅可为6 385，这些集装箱的总重为79 994.42 t。在该情况下，船舶的箱位利用率仅为79.81%。

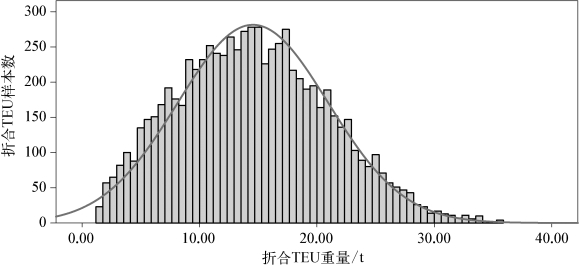
图3-1　样本集装箱单箱重量分布

同时，也可通过所抽取的样本对该航线的总体托运数据进行参数估计。借助SPSS的输出结果（见表3-3）可以发现，样本均值为14.551 4，95%置信区间的一个观察区间为（14.408 1，14.694 6），样本标准差为6.406 22，即可认为总体均值的估计值为14.551 4，总体样本标准差估计值为6.406 22。考虑到当前各企业均采取同样的均一定价机制，上述参数对该港口箱源整体特征的把握也具有相当的参考意义。

表3-3　SPSS计算结果（2）

下面对总体的概率分布进行进一步分析。图3-1中的曲线为根据直方图拟合的正态曲线，从形态上判断，该分布非常接近正态分布，但经SPSS对相关数据进行单样本Kolmogorov-Smirnov检验后发现，其并不符合正态分布。具体检验结论如表3-4所示。

表3-4　SPSS计算结果（3）

经MATLAB编程对样本数据进行进一步分析并进行非参数检验后发现，该总体X近似服从左截尾点为1.55、右截尾点为35.68、均值为14.55、方差为41.04的截尾正态分布。

通过推导，得到左右截尾点分别为a、b的截尾正态分布的密度函数表达式：

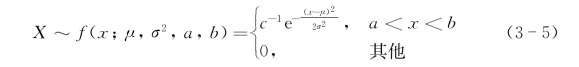
式中，μ是该分布的数学期望；σ2为该分布的方差

基于式（3-5），对X的均值与方差表达式进一步进行推导（显然，当a=-∞，b=+∞时，c=1，式（3-5）即为正态分布的标准表达式）。

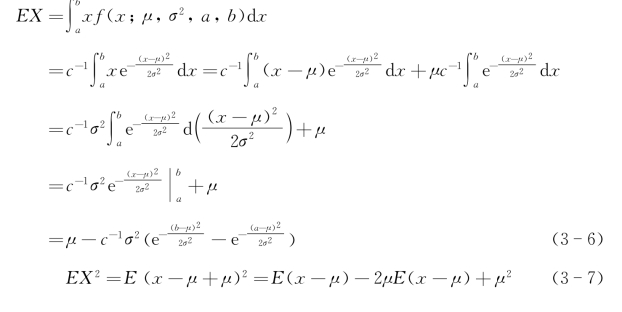
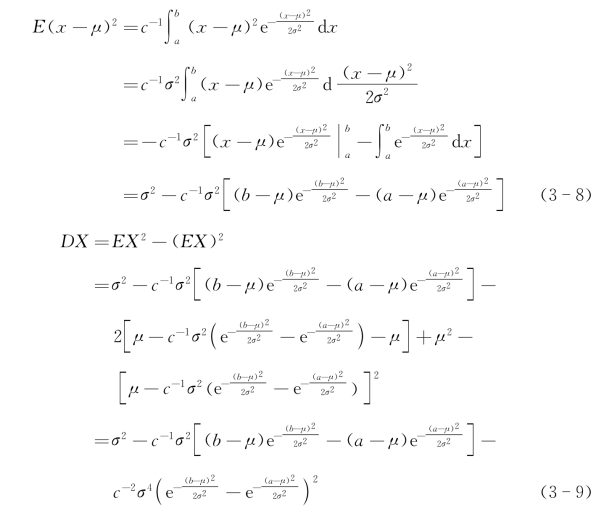
由式（3-6）可知，当b-μ=μ-a或a=-∞，b=+∞时，EX=μ。

式（3-6）、式（3-9）给出了正态分布的数学期望μ、方差σ2与截尾正态分布均值EX、方差DX之间的关系。由样本数据得到EX、DX的估计值后，可进一步利用MATLAB通过式（3-6）、式（3-9）解出μ、σ2的估计值。

为通过提高船舶箱位利用率来提高整体收益，班轮公司需将集装箱单箱重量均值尽量控制在载运船舶的TEU平摊载重吨水平上。另一方面，从船舶积载的角度来看，船舶承运的所有集装箱的重量差异值也最好能够控制在一个相对较低的水平上。由以上两点可知，理想的μ、σ值应比当前的实测数据更小为宜。

由经济学原理可知，如果集装箱运输企业适当降低总重低于基准重量集装箱的运价，并适当提高总重高于基准重量集装箱的运价，则可增加前者的托运量，并同时降低后者，即“偏重箱”的托运量。因此，若托运箱源的重量结构产生上述变化，则该情况下新的μ′、σ′均会向着更有利用于船舶运力利用的方向变化。

如前所述，从班轮公司合理配载的实际需要来看，理想的满载情况下，其所承运的每个集装箱单箱重量最好能相对集中地分布于载运船舶TEU平摊载重吨附近。因此，文献[34]提出的将增收运费的基准重量定为13 t，并对等级区间及其附加收费进行线性均匀划分的建议，并未充分考虑载运船舶的TEU平摊载重吨及箱源重量的客观分布，显然不尽合理。基于“激励相容”的基本原理，班轮公司对更便于其积载，且更有利于提高其收益水平的箱重区间可相应扩大，而对其运力利用有较大负面影响的偏重箱，则应采取更为密集的区间细分，若有必要，还需要配套采用累进费率制。

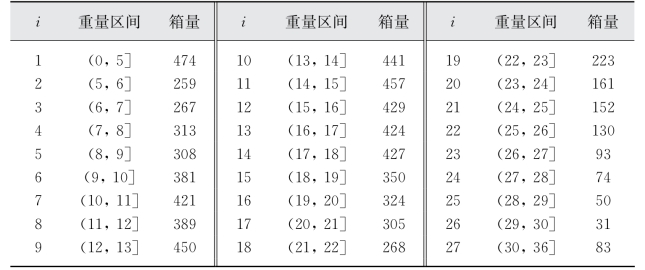
对抽取的样本集装箱单箱重量进行进一步的频度分析，整理得到如表3-5所示结果，其中i为区间序号。

表3-5　样本集装箱单箱重量频度分析

若班轮公司采取均一定价，按800计收运费，则本节样本集装箱的理论最大载运量为6 385，可给运输企业带来的航次收益为5 108 000。

若采用基于集装箱单箱重量的差别定价，则可通过求解式（3-4）给出的优化模型，以确定具体各等级的运费率及相应的载运量。为使问题简化，本章采用如表3-5所示的重量区间作为该算例下基于单箱重量差别定价的等级区间。

2）ΔP i与ΔQ i的映射关系的确定

在真正实现模型应用时，需要通过大量的历史数据来确定ΔP i与ΔQ i的映射关系。为说明问题的核心环节，本节假设该映射关系V i为最简单的线性映射，即ΔQi=V i（ΔP i）=k iΔP i（由经济学原理可知，k i＜0）。本章第6节将针对其他较为复杂的映射关系对优化模型进行进一步的推广。

3）模型求解

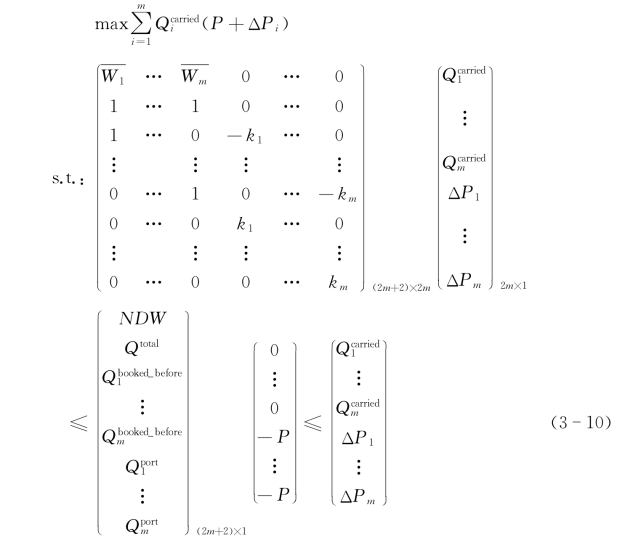
为提高MATLAB的运算效率，先对优化模型进行矩阵化表示，再通过调整k i的取值规律，结合本章样本对不同k i取值规律下的企业收益变化情况进行分析。

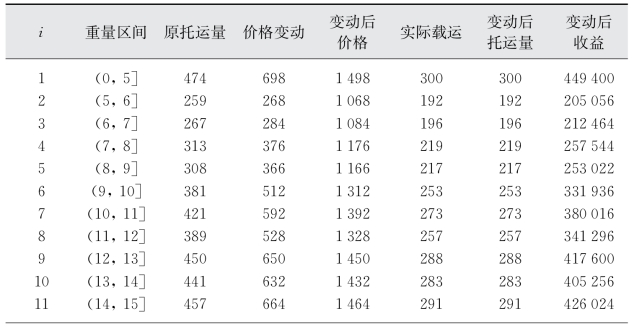
（1）假设k i恒定，取值为-0.25，求解结果如表3-6所示。

表3-6　试验1的优化结果

（续表）

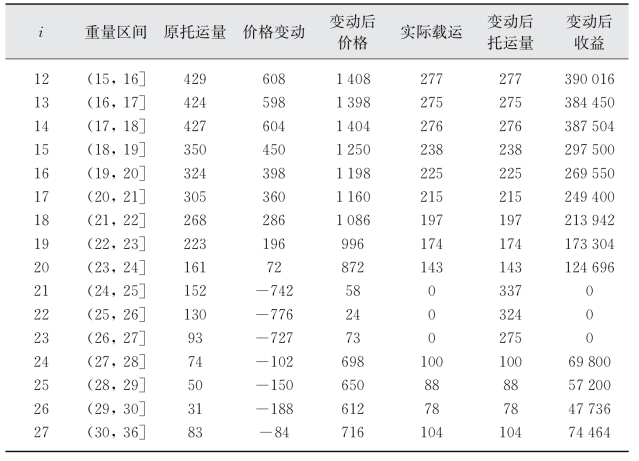
此假设下的航次总收益为6 419 176，高于原先的5 108 000。

（2）假设k i恒定，取值为-0.5，求解结果如表3-7所示。

表3-7　试验2的优化结果

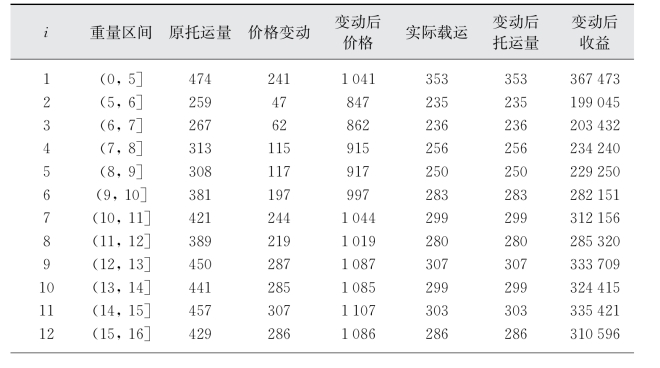
（续表）(www.daowen.com)

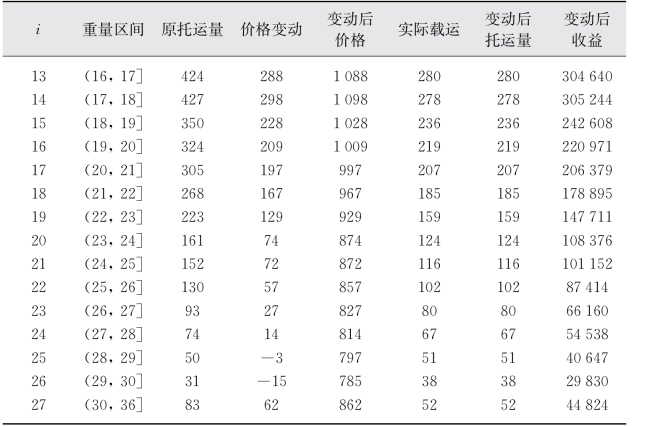
此假设下的航次总收益为5 556 597，也高于原先的5 108 000，但较k i=-0.25时低，说明k i的取值对最优总收益有一定的影响。

（3）假设k i恒定，取值为-2，求解结果如表3-8所示。

表3-8　试验3的优化结果

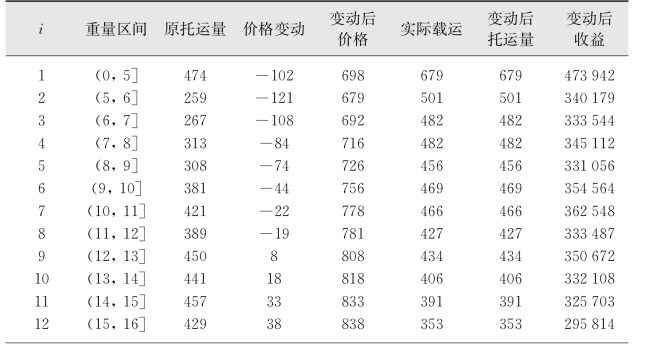
（续表）

此假设下的航次总收益为5 480 113，同样高于原先的5 108 000，但较k i=-0.5时低，进一步表明k i的取值对最优总收益的影响。

同时，若比较试验1、2、3结果中的具体价格变动，可以发现，当k i的绝对值较小时，在不少区间甚至可以通过直接提高运价来增加收益，而随着k i绝对值的逐渐增大，较轻箱的新定价明显低于原先的均一价格。

当然，为初步获得相关基本结论，试验1、2、3仅针对k i取值的最简单情况进行了假设与分析，实际业务中并不太会出现这样的情况。

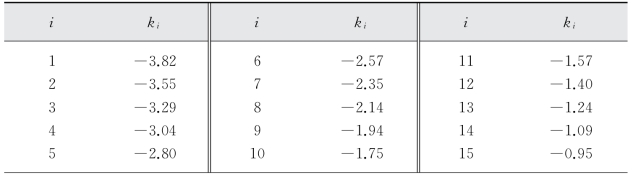
（4）假设k i为非恒定值，取值如表3-9所示，其整体趋势如图3-2所示，即k i绝对值的取值随i的增大而逐渐减小，其拟合曲线总体呈上凸形态。

表3-9　试验4的k i取值

（续表）

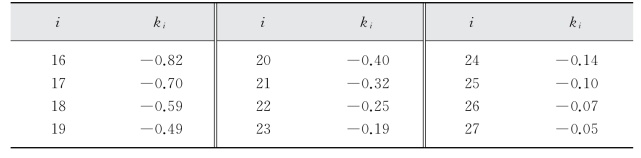
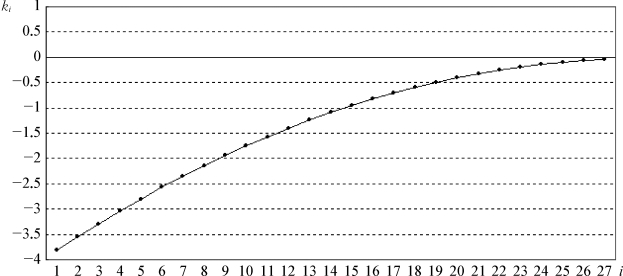
图3-2　试验4的k i取值

此假设下的优化结果如表3-10所示。

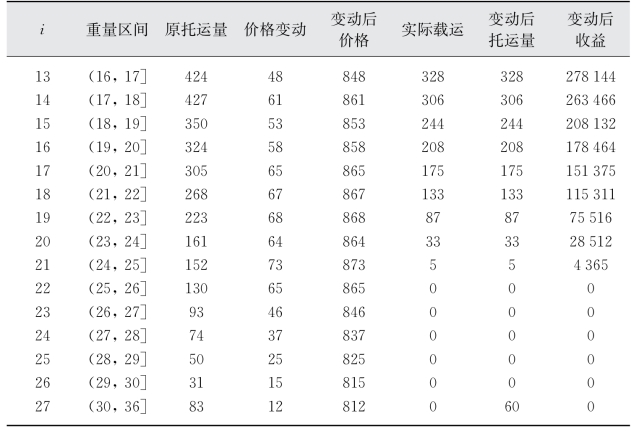
表3-10　试验4的优化结果

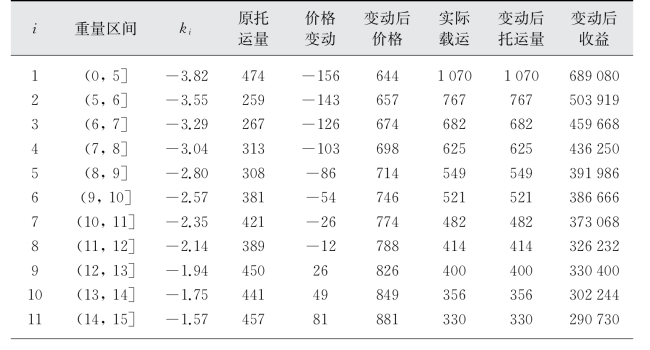
（续表）

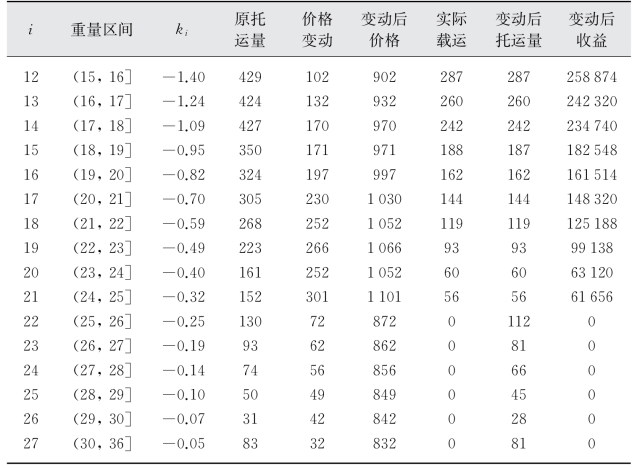
此假设下的航次总收益为6 069 661，高于原先的5 108 000，箱位利用率也有明显上升，达97.55%。

（5）假设k i为非恒定值，取值如表3-11所示，其整体趋势如图3-3所示，即k i绝对值的取值随i的增大而逐渐减小，但其拟合曲线总体呈下凸形态。

表3-11　试验5的k i取值

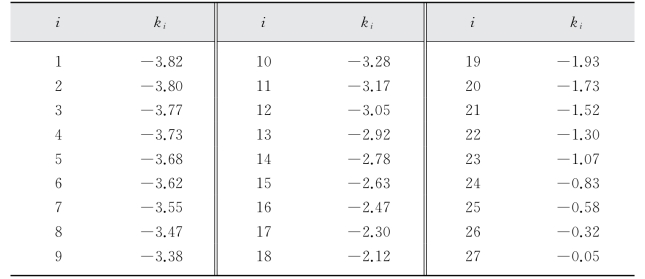
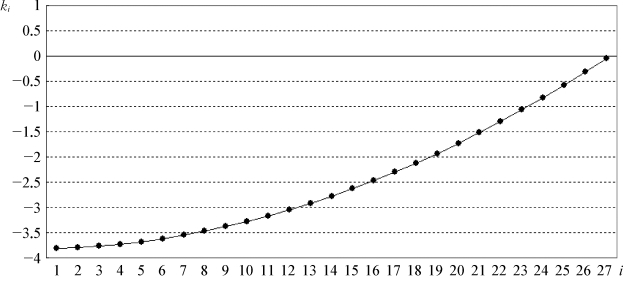
图3-3　试验5的k i取值

该假设下的优化结果如表3-12所示。

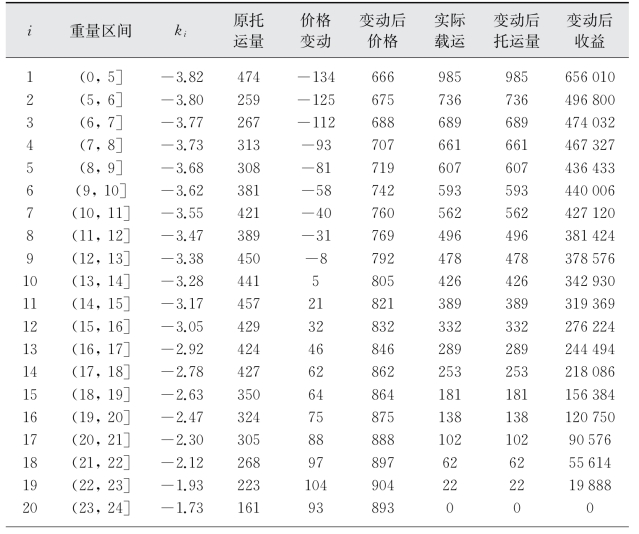
表3-12　试验5的优化结果

（续表）

该假设下的航次总收益为6 002 043，高于原先的5 108 000，箱位利用率达100%。但总体看来，试验5与试验4优化结果的差异并不大，表明只要k i的总体变化趋势相近，k i的具体取值与拟合曲线形态对优化结果的影响并不大。

同时需要说明的是，考虑到各承运人接收偏重箱托运的客观“偏好”，k i绝对值的取值随i的增大而逐渐增大的情况在实践不会出现，因此本书不再赘述。

至此可以发现，k i具体取值的不同会对最优值产生一定影响，但无论k i取值符合何种规律，有一点是可以肯定的，即采用基于集装箱单箱重量的差别定价方式总能获得比原先均一定价方式下更优的收益。

此外，上述五种假设的试验结果还有一个共同特点，即对于向其托运的较轻箱，承运人均应尽可能多地接运，以拉低其所运集装箱的平均重量，为承运单位运价较高的“偏重箱”腾出载重吨指标的空间，这也比较符合目前业务实践的客观规律。

班轮公司在对外公布运价时，可采用前文所述的“基本运费率+偏重箱附加费率”方式。若采用数学试验所选取的频度区间，则可以单箱折算重量5 t作为基本运费的基准重量，随着集装箱单箱折算重量的上升，收取对应的“偏重箱附加费”。

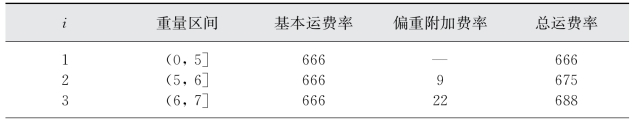
以表3-12为例，若k i取值符合试验5的假设，则实际对货主公布的二部运价本可以制成表3-13的形式。对货主而言，这样的一种二部定价形式要比原先均一定价更为公平合理，也比较接近班轮运价本的传统形式。

表3-13　二部定价运价表简要示例

（续表）

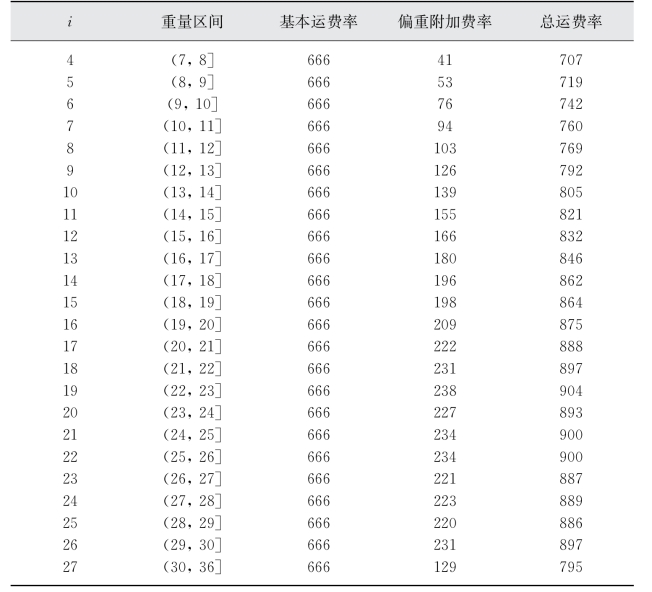
由表3-13可以发现，尽管以单箱折算重量5 t作为基本运费的基准重量，但实际上，直至（12，13]区间，运价都较原先均一运价低，这也从侧面印证了本章建立模型的合理性。

本章在进行数学试验时所取的首区间为（0，5]，如果选择以（0，10]作为首区间，则求得的优化结论与前述结论相仿，但最优值略小。同时，如果班轮公司选择以（0，10]作为优化求解的首区间，则其在公布运价时，基本运费的基准点也需相应改为单箱总重10 t，价格公布形式与表3-13相同。