根据前文中软集的定义可以看出，其并非对论域中所有对象全部信息的全面细致刻画，而是以参数的方式、从多方位的角度对研究对象的分类解读。基于实际决策问题中所掌握对象信息的有限性及审视角度的多样性，以参数化的方式进行对象刻画是符合决策常识的。

在此基础上，Maji等将模糊集理论与软集相结合，于是便产生了如下的模糊软集定义。

令F（U）为给定论域U上的全体模糊子集，E为参数集，且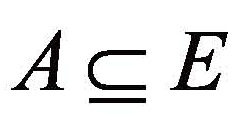。则：

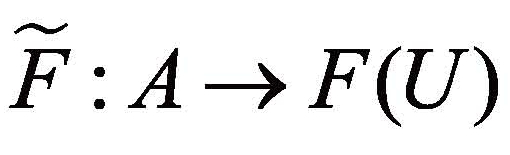定义3-1（Maji，2001）二元组称为论域U上的模糊软集，其中是取值为模糊集的映射，称为模糊软集的近似函数。

与软集类似，取参数e∈A，则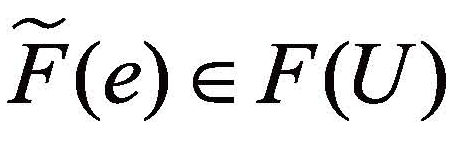称为e-模糊近似集。

基于上述定义，模糊软集可看作给定论域的参数化的模糊集族，是软集的模糊化扩展，是以参数为架构、以模糊信息为表征的对象表达模型。其不再局限于精确软集对对象参数的0/1简单描述，而是以更为灵活的模糊形式表达参数隶属程度，从而可广泛应用于各个领域的不确定状况。

鉴于各类不确定理论与软集的融合发展日趋紧密，尤其是模糊集理论的相关成果源源不断地向软集领域渗透和扩展，对模糊软集决策方法的研究形成了有力的助推。当软集以区间值形式进行表达时，Xiao Zhi（2013）构建了不确定环境中考虑风险态度的决策算法；Peng Xindong（2017）则分别应用遗憾和前景理论解决随机多准则决策问题；Zhang Zhiming（2014）引申Feng Feng的水平软集策略实现区间直觉模糊软集的决策。关于梯形模糊软集，Xiao Zhi（2012）给出了相关定义并提出基于接近度系数的决策排序；而Zhang Zhiming（2013）则应用正负理想解间的定位实现梯形区间二型模糊软集决策。关于直觉模糊软集，Muthukumar（2016）确立了其相似度量和加权相似度量方法，并应用于医学诊断；Wang Fuqiang（2016）则应用模糊测度和D-S证据理论实现决策；Agarwal（2013）给出了广义直觉模糊软集的概念，定义了相似度和大小比较规则。此外，Wang Fuqiang（2014）定义了犹豫模糊软集，并基于得分函数进行规格化决策；王浩伦（2015）将三角模糊软集转化为一般模糊软集以解决失效模式与影响分析风险评估问题。

以上各型模糊软集包含的模糊信息形式各不相同，构建的决策模型也彼此独立，显然难以融合混合模糊信息以支持云制造服务供需认选决策问题的求解。为实时、高效处理决策需求，本章给出了如下一维混合模糊软集的定义。(www.daowen.com)

对于论域X上的模糊集，其中µA ：X→[0，1]，x→µA（x），如果存在两个元素xa，xb ∈X对A的隶属度µA（xa ）和µA（xb）以不同类型的模糊数表达，则可称模糊集A为混合模糊集；否则，A称为非混合模糊集。如：

A={(x1,0.6),(x1,[0.3,0.5)],(x3,(0.6,0.7,0.8,0.9))}

式中，三个元素x1、x2和x3的隶属度分别以一般模糊数、区间值和梯形模糊数进行表达。

与之类似，对于论域U上的模糊软集，如果其中关于对象参数隶属度描述的模糊数类型不唯一，则可称模糊软集为混合模糊软集。

定义3-2 令S（U）为给定论域U上的全体非混合模糊子集，E为参数集，且A⊆E。对于论域U上的混合模糊软集，若的近似函数是取值为非混合模糊集的映射，则称为一维混合模糊软集。取任意参数e∈A，则。

从这一定义可以看出，一维混合模糊软集是混合模糊软集的一种特殊形态，参数之间的模糊隶属度表达各有不同，但同一参数内的表达形式保持一致。对应于云制造服务运作体系中，各主体的属性指标间表示形式不一、指标内部形式统一的形态描述是现实的且可操作的。