麻省理工学院在美国的理工大学中位于榜首，其深厚的理学基础和工程学成就影响着旗下所有院系的研究重心。尤其是斯隆商学院，不同于其他世界著名的商学院，在高层管理者的培养目标上也强调理工科基础的应用，使学生学会科学技术和管理技能，并能够成为侧重技术创新的商业领域高层领导者。因此，在培养领导者最优化决策能力时，斯隆商学院采用数学模型方法，以科学的公式和计算方法帮助管理者进行商业决策。

最优化方法（optimization）是近年来逐渐受到高层管理者和决策者青睐的一种数学方法。在数学领域，它是一种求极值（最大值或最小值）的方法，就是在一定的方程等式或不等式条件中，通过计算推导，使目标函数达到最大值或者最小值。从经济学的角度对这个命题的解释是这样的：这里的等式或者不等式在组织中，就相当于在一定的人力资源、物力投入、财力分配的条件下，保证经济效果（或者商业价值）追求最大化。或者情况相反，在完成既定的经济或者生产任务下，使组织投入的财力资源、物质资源和人力资源最少。

现在，越来越多的研究者和管理者将最优化方法应用于寻找各种系统的优化途径和方案，以便为组织或系统的管理者和决策者提供科学的决策依据。在斯隆商学院的高层管理者能力培养过程中，更是将最优化方法应用于制造产业、交通运输、物流、计算机科学、项目管理、金融、电子商务等众多商业领域。通过在这些领域中对最优化方法的运用和实践，将所调查的一些应用程序优化，掌握具体的决策模型和算法，例如网络流线性规划、动态规划、整数规划和决策树。具体在企业中，就是完成最优设计、最优计划、最优管理和最优控制四个方面的命题。

斯隆商学院的研究者一直在探索适用于更广泛领域的领导者能力特质，因此，不论是管理者的顾客观，还是员工观，斯隆商学院长久以来探索的不是管理者可以选择的管理策略是什么，而是努力发现其中的通用原则。在对最优化方法实验和应用的过程中，斯隆商学院发现了其在决策过程中的普遍适用性，因此，在培养方案中极力推崇。

他们认为最优化方法无处不在，它能够解决组织的运营管理、市场营销、战略规划，以及金融领域和工程设计实施等方面的决策和管理问题。例如，设计选择适合的工程设计参数，使工程方案既满足要求又花费较低的成本；计算能够提高产值和利润的生产方案；对企业资源进行合理规划，同时满足各个部门的发展需要，并获得最大的经济效益；甚至包括在军事指挥中，确定最有利于全局、消灭敌人保全自己的最佳作战方案等等。但是在不同的领域，进行不同的决策和规划时，所采取的最优化运算模型是不同的，其中主要包括线性规划、整数规划、非线性规划、决策树和动态编程。

与此同时，在斯隆商学院的课程设置中，关于最优化方法的内容，有探讨最优化方法的算法模型内容和应用的“最优化导论”；具体探讨线性规划模型的基本原理及其复杂的实际应用问题的“系统最优化”；以及关注网络模型如何解决最短路径问题、最大流量问题、最少成本流量问题和多元物品流量问题等子问题的“网络最优化”；在制造业系统中进行建模、优化和应用的模拟实践的“制造领域系统最优化与分析”；以及关于最优化的经典篇章和最新理论的“最优化书报讨论”。

对主题进行研究的教授包括罗伯特·弗罗因德教授（Robert Freund），主要致力于通过数学模型提升管理系统的性能，使之更加优化，其研究涉及企业中的人员调度、容量规划和投资组合选择几个方面，他在决策树、概率、统计推断、回归模型、仿真模型、线性和非线性优化模型方面有独到的见解；史蒂夫·格雷斯教授（Stephen Graves），主要探索在生产制造系统和销售模式中如何运用最优化模型和方法，其目前的研究方向是供应链优化、生产和容量规划、供应链体系中战略库存定位；迪米特里斯·伯特西马斯教授（Dimitris Bertsimas），斯隆商学院的管理学教授，同时也担任波音公司的管理者，研究重心集中在优化系统的数据分析和应用策略，研究范围包括金融领域和医疗行业，攥写了关于线性优化模型、数据分析处理的专著和科学论文110多篇；詹姆斯·维列夫教授（James Orlin），专研于网络模型和组合优化，他的研究应用于开发和改进航空调度、铁路调度、物流、网络设计、电信、库存控制和营销等管理领域的具体方法。

作为企业的高层管理者，在运用最优化算法的过程中，理解算法的原理和算法运用的含义，要比掌握算法的流程更重要。以网络模型在完成“人员指派决策”时为例，斯隆商学院的约翰·温杜尔教授（John Vande Vate）做了一个案例假设，以便管理者更好地运用最优化方法。在下述案例中，为了便于管理者了解最优化方法的应用，将不进行算法介绍，只进行原理解构。

首先，案例中假设这是一个分部跨欧洲四国的大型汽车生产厂商，四个分厂分别位于德国莱比锡、法国南锡、比利时列日和荷兰提尔堡。现在总部将布置一项新的生产任务，并需要委派一位副总裁到四个分厂进行指导、考察和审核生产进程和效果。那么作为公司的总裁，需要考虑派什么样的人去执行这个任务，这个问题涉及人才的选择，所以副总裁对新生产任务要具有一定的知识储备；

其次，考虑四个分厂需要什么样的指导，与副总裁具有的知识是否相符；

第三，因为四个分厂在不同的国家，那么副总裁是否具有语言交流能力等；

第四，考虑如何使这次指派行动的成本最低，即如何设定副总裁完成这个任务的时间，能够利用的资源有多少，以及是派一个副总裁分别到四个分厂进行指导和考察，还是同时指派四个副总裁完成这项任务。

在所需要考虑的因素中，其所有的选择原则只有一个：成本最小而效益最大。因此，首先预估指派成本，分别列出到不同厂商所涉及的部门及付出的成本。如下表所示：

表4-1　预估指派成本

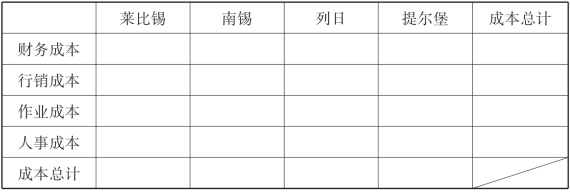
在上表中，横列和纵列中各有一个“成本总计”，这是对其所对应的前面（或上面）的成本预估的总计。按照网络模型，接下来进行工具计算。最优化算法是一种数学方法，其运算需要的软件在Excel中就能够实现。(www.daowen.com)

在Excel中默认有一个solver插件（求解器，或规划求解器），在使用之前需要激活，激活的方式在不同的版本中不同，以Excel2003为例：首先在“工具”下拉菜单中点击“加载宏”，弹出对话框后，在“分析工具库”和“规划求解”前打勾，点击确定。然后在“工具”下拉菜单中能看到“规划求解”，点击，将弹出“规划求解参数”菜单（如下图所示），之后就可以使用了。

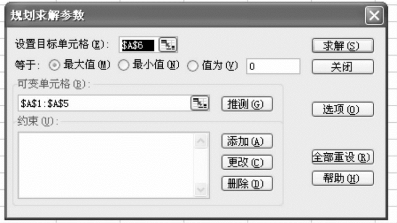
图4-1　Excel中规划求解菜单示例

上表中的“设置单元格”、“等于”、“可变单元格”、“约束”几个位置可以根据实际情况进行选择，另外，点击“求解”选项，还可继续选择限定运算条件。其中的操作属于数学计算范畴，本章中不做赘述。

展示上述计算过程，是为了阐明最优化算法的应用。而在案例中设定的是一个拥有跨国分工厂的大型汽车生厂商，这并不意味着最优化的网络模型只适用于大型公司，而是在这样的大环境中比较方便理解。

事实上，最优化方法适用于各种类型的企业、各种情境中的决策分析。然而，作为众多其他学科进行运算和验证的基本工具——统计学，一直在表明这样一个立场：数据是根据公式和运算操作得到的结果，其数值对决策有参照意义，却没有决定性力量。约翰·温杜尔教授在讲述这个案例的运算过程中，还提到一个影响最佳结果的因素：情感和人事偏好。最优化算法能够算出哪种方案的成本最低，但是什么样的人完成这个任务的效率更高呢？这就要回顾第三章第一节的内容（人与公司的关系），麻省理工斯隆商学院国际研究中心的罗伯特·布德里教授在其最新的研究中提出，“关系”对事物存在微妙的助力。根据他在微软中国实验室的观察和分析，比尔·盖茨在任命中国区实验中总裁时，李开复并不是他唯一的候选人，在衡量了必要的投入消耗之后，让比尔·盖茨最后做决定的是李开复的华裔背景，他认为中国的商业氛围和商人关系特点，决定了一个华裔执行总裁能够更好的胜任。因此，管理者在进行最后决策时，如果面对成本预估情况相似的几个方案或者候选人，一定要理智地进行效果最佳的选择。最优化算法提供给管理者的只是一种推理方法，而不是进行决策的必要条件。

在企业中，管理者与工程师不断地企图将复杂系统的设计与运作最优化，斯隆商学院对于这类课程的教授，秉承的是鼓励管理者使用最优化模型，以便支援管理者与工程师在不同的决策环境下做最好的决策，这门课程属于最优化算法的应用指导。斯隆商学院的学者通过不同应用领域（或产业）的案例，说明了最优化技巧如何使用。在斯隆商学院，几乎所有的教授和研究者都还有另一个身分——大型技术型企业的顾问，他们参与企业的决策，为企业管理者制定政策，选择方案提供重要意见，同时也将不同的方法在现实企业环境中验证。他们通过各自研究确认最优化算法的应用的机会，以及管理最优化决策支持性工具应用的技巧。

管理者在决策的过程中需要掌握最优化模型与求解的技巧，这些模型包括线性模型、非线性模型、整数模型、网络最优化与启发式算法等。不同的算法模型应用领域不同，对结果的解释也不同。其中非线性优化模型主要应用于运输领域，包括交通平衡、交通管理、收入管理及定价，金融——资产组合管理，工程领域的数据网络和路径选择、样式分类，制造领域的资源配置和生产规划。启发式算法则又可以细化成近似算法、局部搜索和模拟退火，近似算法是通过不断的运算，将解与最优化结果不断靠近的方法；局部搜索是通过修改细小的部分，将现在的解换成更好的解直至达到最优解；模拟退火则是在一个大的搜寻空间内找寻最优解。

此外，管理者还要根据运算工具的结果解释与分析由模型所求出的解，分析不同的限定条件所代表的现实情况，并作出最终的决策。麻省理工学院试图引导未来的管理者更多地关注这个算法，学习算法中的几个关键意义，而不是注重算法工具的普及。

一个Excel可以给出一些算法的解，解决模型问题，但是任何有意义和无意义的数字在算法模型中都能够得到一个解。判断解的过程和含义，做出理智判断。在利用最优化算法之前，首先要明白，很多企业问题的表面和实质存在差距。有时候一些看似容易的问题其本质是复杂棘手的，涉及企业的众多环节，有时候一个看似复杂的问题其本质却是能够简化的，这些可以通过最优化算法进行区分。因为带入公式和工具时，需要用数字代表不同的环节，能否准确快速地找到这些数值，就能够对于得到数值的对应部门进行评估和考察判断。这样转化之后，利于管理者洞察问题，统计出现的困难，计算决策。

第二，正确理解最优化算法是解释和应用最优化算法的解的第一步。运算过程中，不同的“约束”（见对Excel话框中的标签）得到的解不同，不能够单纯根据结果数字进行比较，还要考虑精确度、运算时间、允许误差范围等等。

第三，最优化算法模型并不唯一，通过理解内部工作的最优化算法应用，企业和管理者可以修改那些最优化模型中，适合自己企业发展和规划的新最优化算法。现在的最优化模型有很多种，很多都是研究者在实际的应用过程中不断修改和完善的，任何的应用都要以实践的检验结果为准绳。

最优化方法恰如其名，最大的特点就是优化，它为问题提供了一个最佳的解决方案，同时还提供了一个简洁的证明过程。数字的计算过程，就是规划应用的缩影。即将复杂的管理转化为清晰的数字。

斯隆商学院的一位管理学教授说过：我们构建模型不是为了寻找一个现实的镜子，它能够反映的只是部分现实。如同上文所述，数字是固定刻板的，但是管理者是灵活的。任何数学范围内的建模，其本质在管理科学中都是为了提供决策支持，让管理者更直观地看到决策和规划的结果，可以通过分析模型来确定哪些数据是最重要的，哪些数据只能够小范围内改变与影响决策，从而得到决策或规划过程中哪些环节会影响最后的最优解，哪些环节必须在决策过程中给予关注。

一个有用的好的方法模型，允许管理者随时进行修改，添加或者删减环节。甚至能够是在统一决策过程中，同时包含不同的优化算法。随着现代科技的发展，在电子商务应用中，通过计算机能够同时在短时间内解决成千上万的模型运算。从技术上来说并不困难，但是如何解释，如何辅助管理者的洞察分析，却是管理者的难题。所以，了解一个方法，掌握一个方法，并不能够万事亨通。运用一个方法，将其发挥最大的价值，才是真正的策略。