1.调节效应分析

一般而言，如果因变量Y和自变量X的关系是变量M的函数，则称M为调节变量（温忠麟等，2005），即Y与X的关系受到变量M的影响，变量M对Y与X的关系有调节作用，具体模型如图6.7所示。

图6.7　调节效应示意图

资料来源：温忠麟，侯杰泰，张雷.调节效应与中介效应的比较和应用[J].心理学报，2005，37（2）：268-274.

温忠麟等（2005）对调节效应的分析方法做了比较全面的阐述，认为当自变量和调节变量均为连续变量时，在进行调节效应分析之前，应将各变量进行去中心化处理。因此，本节所有涉及变量（除人口统计变量）均已进行去中心化处理。此外，根据相关分析，人口统计学变量与诸多变量均相关，因此在做回归分析之前，有必要对人口统计学变量进行控制。具体而言，在引入控制变量之后，依次对自变量、调节变量和因变量之间的关系进行回归分析，且回归系数均为标准化的β值。

2.认知年龄的调节效应

表3.39为认知年龄对X 1、X 2和Y的调节效应

表6.39　认知年龄对X1、X2和Y的调节效应

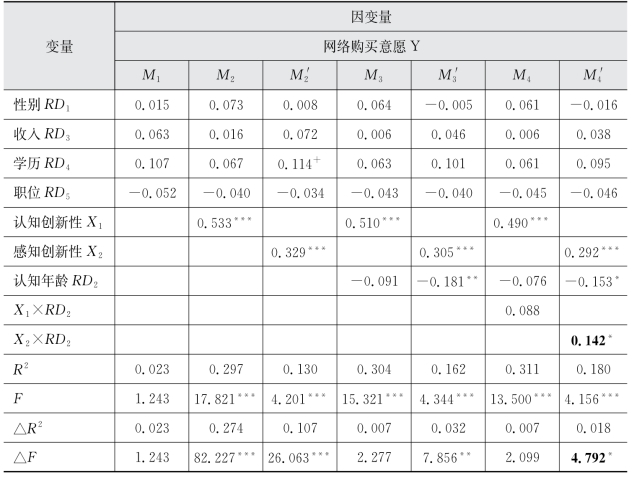
从表6.39可以看出，在控制了除认知年龄以外的其他人口统计变量的基础上，乘积项X 1×RD 2的系数不显著，X 1×RD 2对Y（网络购买意愿）不存在显著影响。控制变量和X 1解释了因变量29.7%的方差变异。在此基础上，RD 2解释了因变量0.7%的方差变异，乘积项只解释了因变量0.7%的方差变异。通过F和△F检验可知，解释变量对因变量不存在显著效应，即认知年龄对认知创新性和老年消费者购买意愿之间的关系不存在调节效应，假设H10a未得到验证。乘积项X 2×RD 2的系数在0.05水平下显著，X 2×RD 2对Y存在显著影响。控制变量和X 2解释了因变量13.0%的方差变异，在此基础上，RD 2解释了因变量3.2%的方差变异，乘积项解释了因变量1.8%的方差变异，通过F和△F检验可知，解释变量对因变量存在显著影响，即认知年龄对感知创新性和老年消费者购买意愿之间的关系具有调节作用，假设H10b得到验证。

3.风险意识的调节效应

（1）心理风险的调节效应（见表6.40）。

表6.40　心理风险对X1、X2和Y的调节效应(www.daowen.com)

注：M 1、M 2、M 3、M 4是检验心理风险（M 3a）对认知创新性（X 1）和老年消费者网购意愿之间的关系是否存在调节效应的模型；M 1、M 2′、M3′、M4′是检验心理风险对感知创新性（X 2）和老年消费者网购意愿之间的关系是否存在调节效应的模型。

从表6.40可以看出，在控制人口统计变量的基础上，乘积项X 1×M 3a、X 2×M 3a的系数均不显著，说明X 1×M 3a、X 2×M 3a对Y不存在显著影响。因而，心理风险对消费者创新性和老年消费者网购意愿之间的关系不存在调节效应，假设H11a1、H11b1未得到验证。

（2）社会风险的调节效应（见表6.41）。

表6.41　社会风险对X1、X2和Y的调节效应

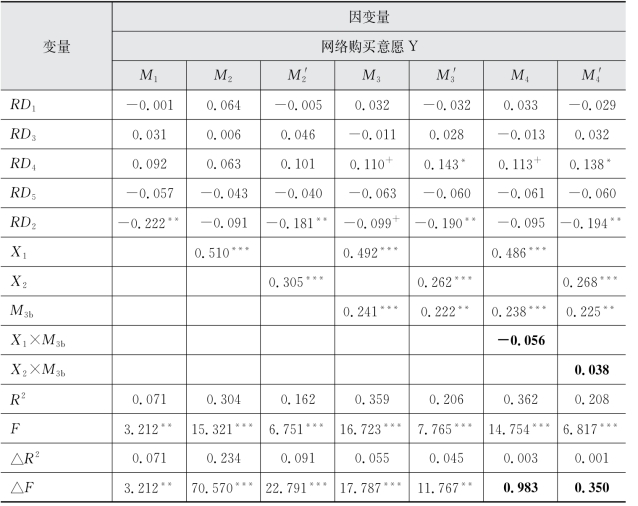
注：M 1、M 2、M 3、M 4是检验社会风险（M 3b）对认知创新性（X 1）和老年消费者网购意愿之间的关系是否存在调节效应的模型；M 1、M 2′、M 3′、M 4′是检验社会风险对感知创新性（X 2）和老年消费者网购意愿之间的关系是否存在调节效应的模型。

从表6.41可以看出，在控制人口统计变量的基础上，乘积项X 1×M 3b、X 2×M 3b的系数均不显著，说明X 1×M 3b、X 2×M 3b对Y不存在显著影响。故而，社会风险对消费者创新性和老年消费者网购意愿之间的关系不存在调节效应，假设H11a2、H11b2未得到验证。

（3）功能风险的调节效应（见表6.42）。

表6.42　功能风险对X1、X2和Y的调节效应

注：M 1、M 2、M 3、M 4是检验功能风险（M 3c）对认知创新性（X 1）和老年消费者网购意愿之间的关系是否存在调节效应的模型；M 1、M 2′、M 3′、M 4′是检验功能风险对感知创新性（X 2）和老年消费者网购意愿之间的关系是否存在调节效应的模型。

从表6.42可以看出，在控制人口统计变量的基础上，乘积项X 1×M 3c的系数在0.05水平下显著，X 1×M 3c对Y存在显著影响。控制变量和X 1解释了因变量30.4%的方差变异，在此基础上，M 3c解释了因变量1.1%的方差变异，乘积项解释了因变量1.3%的方差变异。通过F和△F检验可知，解释变量对因变量存在显著影响，即功能风险对认知创新性和老年消费者网购意愿之间的关系存在调节效应，假设H11a3得到验证。乘积项X 2×M 3c的系数均不显著，说明X 2×M 3c对Y不存在显著影响。所以，功能风险对感知创新性和老年消费者网购意愿之间的关系不存在调节效应，假设H11b3未得到验证。