实验名称：主要资产定价模型实验

实验目的与要求：

1.熟悉资本资产定价模型结构，绘制证券报酬率与β系数的关系曲线。

2.掌握β系数的含义，研究利用β系数测算证券的风险。

3.理解资本资产定价模型与套利定价模型在定价方法上的区别。

实验条件：

1.预习课本第2章第2节。

2.收集企业资本资产定价模型的相关资料。

3.计算机及相应软件。

4.计算器、三角板，资料记录卡（作业纸）。

5.常用货币时间价值系数计算表。

实验性质：综合性实验

实验学时：2

实验内容：

1.分析资本资产定价模型结构因素，绘制证券报酬率与β系数曲线。

2.分析研究β系数的含义，利用β系数测算证券的风险。

3.研究资本资产定价模型与套利定价模型在定价方法上的主要区别。

实验步骤与实验方法：

1.分析资本资产定价模型的一般形式，绘制证券报酬与β系数曲线。

2.分析研究β系数的经济含义，利用β系数测算证券的风险。研究β系数对证券报酬的影响。

3.分析资本资产定价模型与套利定价模型在定价方法上的主要区别。

实验原理：

由风险收益均衡原则中可知，风险越高，必要收益率也就越高，多大的必要收益率才足以抵补特定数量的风险呢？市场又是怎样决定必要收益率的呢？一些基本的资产定价模型将风险与收益率联系在一起，把收益率表示成风险的函数，这些模型包括：①资本资产定价模型；②多因素定价模型；③套利定价模型。

市场的预期收益是无风险资产的收益率加上因市场组合的内在风险所需的补偿，用公式表示如下：

R_M=R_F+R_P

式中 R_M——市场期望报酬率；

R_F——无风险资产的报酬率；

R_P——投资者因持有市场组合而要求的风险溢价。

在构造证券投资组合并计算它们的收益率之后，资本资产定价模型（Capital Asset Pricing Model，CAPM）可以进一步测算投资组合中的每一种证券的收益率。

资本资产定价模型建立在一系列严格假设基础之上：

1）所有投资者都关注单一持有期。通过基于每个投资组合的预期收益率和标准差在可选择的投资组合中选择，他们都寻求最终财富效用的最大化。(www.daowen.com)

2）所有投资者都可以以给定的无风险利率无限制地借入或借出资金，卖空任何资产均没有限制。

3）投资者对预期收益率、方差以及任何资产的协方差评价一致，即投资者有相同的期望。

4）所有资产都是无限可分的，并有完美的流动性（即在任何价格均可交易）。

5）没有交易费用。

6）没有税收。

7）所有投资者都是价格接受者（即假设单个投资者的买卖行为不会影响股价）。

8）所有资产的数量都是确定的。

资本资产定价模型的一般形式如下：

R_i=R_F+β_i（R_M-R_F）

式中 R_i——第i种股票或第i种证券组合的必要报酬率；

R_F——无风险报酬率：

β_i——第i种股票或第i种证券组合的β系数；

R_M——所有股票或所有证券的平均报酬率。

证券报酬率与β系数的关系如图2-2所示。

风险规避的程度对风险较大的证券影响更为明显。例如，图2-3中一个β系数为0.5的股票的必要报酬率只增加1个百分点，即从8%增加到9%；而一个β系数为2.0的股票的必要报酬率却增加了4个百分点，即从14%上升到18%。

实验课题：

【资料】

（1）柯特林公司股票β系数为0.5时，风险报酬率利率为2%，市场股票的无风险报酬率为6%；当β系数为1.0时，风险报酬率利率为4%；当β系数为2.0时，风险报酬率利率为8%。

（2）柯特林公司股票β系数为2.5，无风险利率为6%，市场上所有股票的收益率为10%。

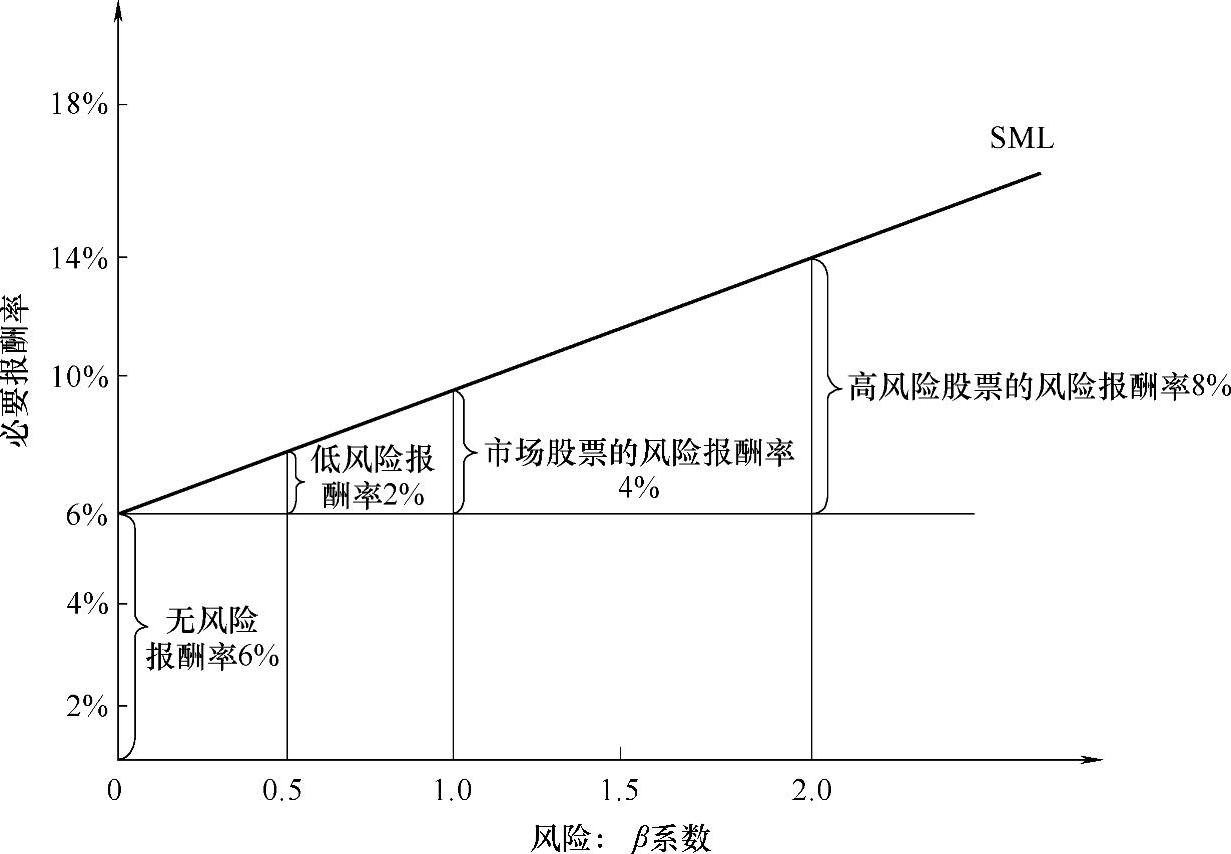
图2-2 证券报酬率与β系数的关系

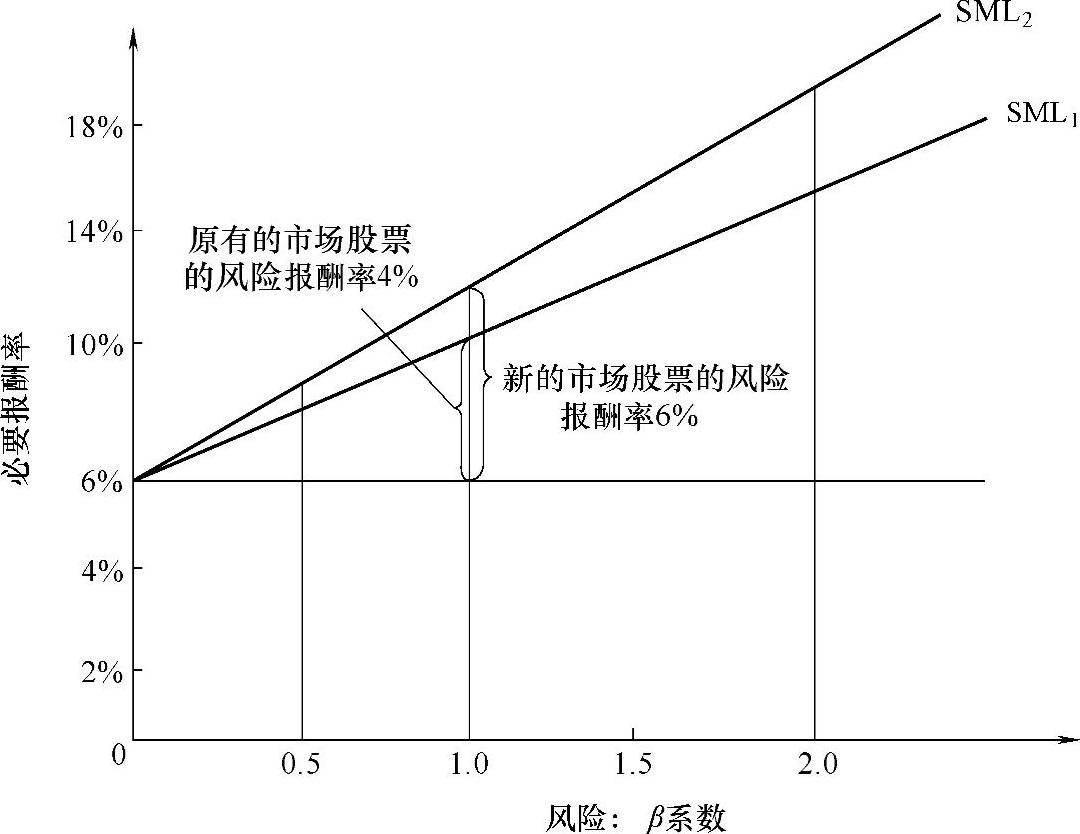
图2-3 风险规避对证券报酬率的影响

（3）柯特林公司股票β系数上升为3.5，无风险利率为6%，市场上所有股票的收益率为10%。

【要求】

（1）绘制柯特林公司股票的证券报酬率与β系数的关系图。

（2）计算柯特林公司股票的证券报酬率。绘制证券市场线SML₁。

（3）计算β系数上升后的柯特林公司股票的证券报酬率。绘制证券市场线SML₂。

（4）由β系数的变动分析风险规避对证券报酬率的影响。