（一）层次分析流程

将主题酒店顾客感知服务质量评价的关键要素分解成简明的等级系统，经过成对比较评估及矩阵运算，求得等级因素与评估的优先顺序，层次分析流程如图（4-7）：

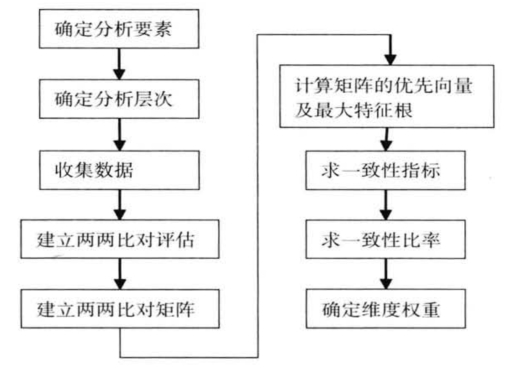
图4-7　层次分析流程图

（二）关键因子层次模型

图4-8　层次结构模型

（三）指标权重的计算

本次研究中的数据主要来自于主题酒店经营管理人员、从事主题酒店研究的专业人员等，通过请教访谈的方法，运用T.L.Saaty提出的“1-9标度法”，获取专业人士对以上关键因子的评价。回收问卷后对首先剔除不符合要求的问卷，然后标准差法剔除差异性比较大的数据，再综合成群体判断矩阵，利用计算出各判断矩阵的最大特征根λ max和相应的权重向量W，并进行一致性检验。

此次研究中用AHP中“特征根法”来计算权重：

AW=λmaxW

其中式中λmax是A的最大特征根，W是相应的特征向量，所得到的W经归一化后就可作为权重向量。利用Matlab计算出各判断矩阵的最大特征根λmax和相应的权重向量W，并进行一致性检验。利用Matlab求解的具体过程和代码如下：

1.求最大特征根λmax

利用Matlab求特征根的方式：表示输入矩阵，即求矩阵a的最大特征根

［ x ，lumda］ = eig （a）

r = abs （sum （lumda））

n =find（r= =max（r））

max_lumda_a = lumda（n，n）

其中，max_lumda_a就是最大特征根。

2.求解一组指标的权重

最大特征根所对应的特征向量：Max_x_a=x（：，n）

利用特征根方法，aw=λmaxw

则在Matlab中的实现语句为：

W_a_1 = max_x_a/sum（max_x_a）

3.求一致性指标CI

根据公式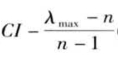，（n为判断矩阵的阶数）

则在Matlab中求一致性指标CI的值的语句为：

CIa=（max_lumda_a_n）/（n-1）

即求矩阵a对应的CI的值，n为矩阵的阶数

4.求一致性比率CR

又根据公式，

查找相应的平均随机一致性指标RI，可查找Saaty给出了RI的值

表4-3　平均随机一致性指标R.I.

则在Matlab中求矩阵n对应的一致性比例CR的值的语句为：

CRa = CIa/RIa

由此，可根据矩阵求出最大特征根λmax、权重W、一致性指标CI和一致性比率RI。结果如下面几个表所示：（见表4-4至表4-14）

表4-4　构建成对比较矩阵（U-A）

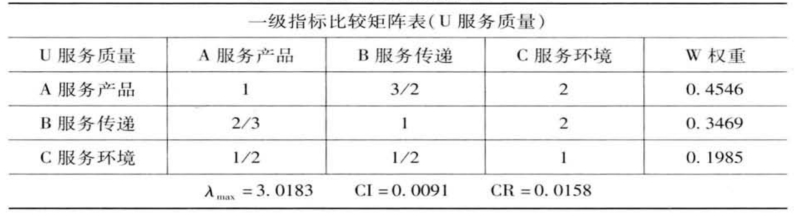
表4-5　构建成对比较矩阵（A-A1）(www.daowen.com)

表4-6　构建成对比较矩阵（B-B1）

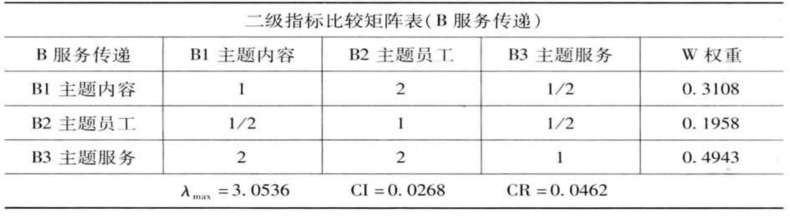
表4-7　构建成对比较矩阵（C-C1）

表4-8　构建成对比较矩阵（A1-A11）

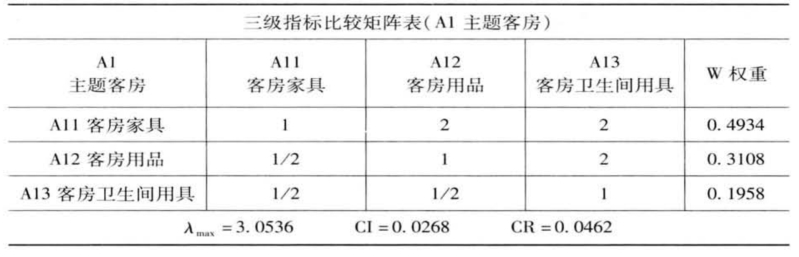
表4-9　构建成对比较矩阵（A2-A21）

表4-10　构建成对比较矩阵（B1-B11）

表4-11　构建成对比较矩阵（B2-B21）

表4-12　构建成对比较矩阵（B3-B31）

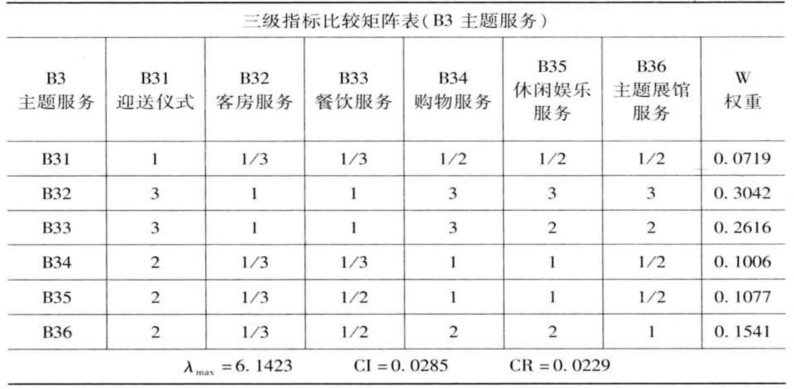
表4-13　构建成对比较矩阵（C1-C11）

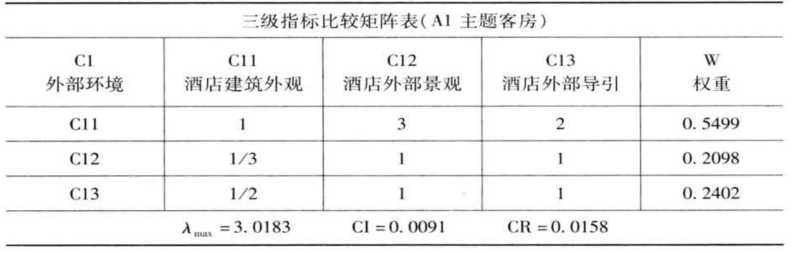
表4-14　构建成对比较矩阵（C2-C21）

通过上面的计算得出以上判断矩阵值的一致性比率CR≤0.1，这说明判断矩阵具有较好的一致性，通过一致性检验。

（5）计算组合权重并做一致性检验

我们根据组合权重的计算公式：

则第三层、第四层（关键因子）相对于第一层（感知服务质量）的组合权重为：

W3=W3 × W2

求出层次的组合权重，并进行各评价因子的排序，如表（4-15、4-16）所示。

表4-15　二级指标组合权重列表

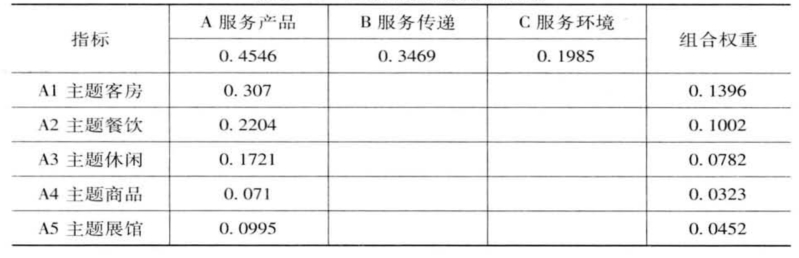
续表

表4-16　三级指标组合权重列表

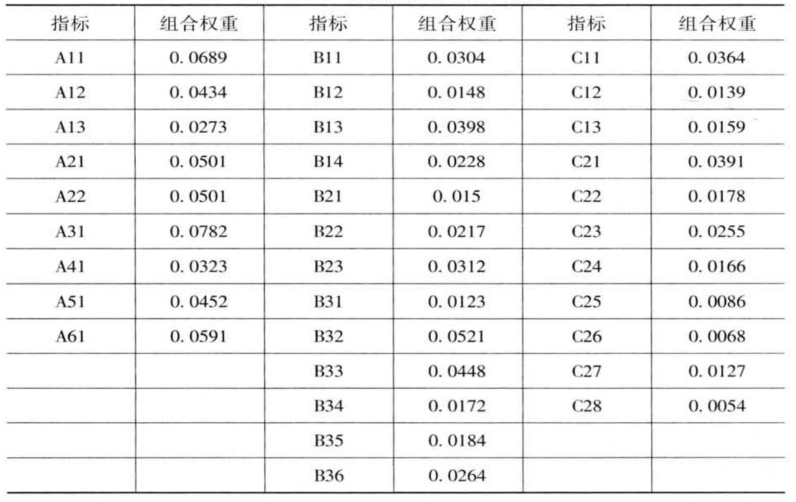
为便于查看，笔者将二级、三级各项指标按权重排序，结果如下：（见表4-17、4-18）

表4-17　二级指标组合权重排序表

续表

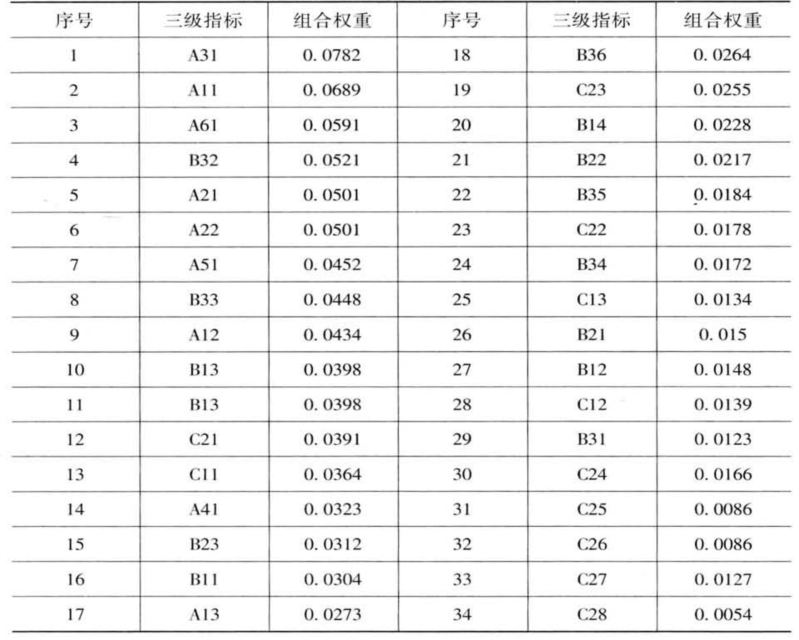
表4-18　三级指标组合权重排序表