二阶常系数非齐次线性微分方程的一般形式为

方程（10.14）对应的齐次线性微分方程是

1.二阶常系数齐次线性微分方程的通解

由齐次线性微分方程通解结构定理2可知，只要求出方程（10.15）的两个线性无关的解，就可以得到其通解.问题是如何求得它的两个线性无关的特解呢？注意到方程（10.15）的左端是关于y″，y′，y的线性关系式，且系数为常数，而λ为常数时指数函数eλx和它的各阶导数最多只差一个常数因子，因此我们用y＝eλx来尝试，看能否取到适当常数λ，使y＝eλx是方程（10.15）的解.

对y＝eλx求导，得y′＝λeλx，y″＝λ2eλx.将y″，y′，y代入方程（10.15），得

由于eλx≠0，所以

由此可知，只要λ是代数方程（10.16）的根，函数y＝eλx就是微分方程（10.15）的解.我们把代数方程（10.16）叫作微分方程（10.15）的特征方程，其根称为微分方程（10.15）的特征根.

根据一元二次代数方程的求根公式，可得两个特征根为

下面按特征根的三种不同情况，分别讨论方程（10.15）的通解求法.

仍为微分方程（10.15）的两个线性无关的解.则方程（10.15）的通解为

综上所述，求二阶常系数齐次线性微分方程的通解的步骤如下：

第一步：写出齐次线性方程相应的特征方程，求出特征根；

第二步：根据两个特征根的三种不同情况，写出微分方程的通解.为方便使用，将上面的结论做成如表10.1所示.

表10.1

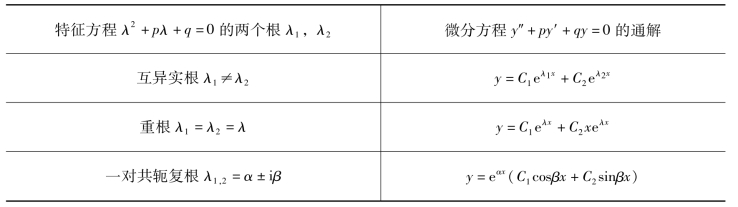
例2　求方程y″－4y′＋3y＝0的通解.

解　该方程所对应的特征方程为

其特征根为互异实根λ1＝1，λ2＝3，故所求方程的通解为

例3　求方程y″＋4y′＋4y＝0满足初始条件＝0的特解.

解　该方程所对应的特征方程为

其特征根为重根λ1＝λ2＝－2，故所求方程的通解为

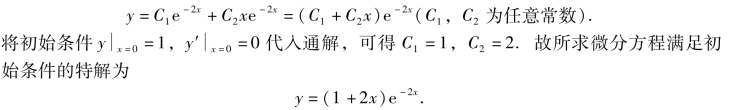
例4　求方程y″－2y′＋5y＝0通解.

解　该方程所对应的特征方程为

其特征根为一对共轭复根λ1，2＝1±2i，故所求方程的通解为

2.二阶常系数非齐次线性微分方程的通解

二阶常系数非齐次线性微分方程的通解归结为求它所对应的齐次线性微分方程的通解和它自身的一个特解.从前面的讨论可以看到，对应的齐次线性微分方程的通解总能求得，剩下的事情就是求出非齐次线性微分方程的一个特解.对此我们不做一般讨论，仅对四种常见类型的f（x），不加证明地介绍用待定系数法求特解的方法.

类型1　f（x）＝Pm（x），其中Pm（x）为m次多项式.

由于方程右端f（x）为多项式，故设方程（10.14）的特解为多项式Q（x），将其代入方程，得

要使上式恒成立.

当q≠0时，Q（x）应为m次多项式，故可设(www.daowen.com)

其中A0，A1，…，Am是待定系数.

当q＝0且p≠0时，Q（x）应为m＋1次多项式，故可设

其中A0，A1，…，Am是待定系数.

当p＝q＝0时，Q（x）应为m＋2次多项式，故可设

其中A0，A1，…，Am是待定系数.这时，由于p＝q＝0，方程（10.15）成为y″＝Pm（x），其通解也可对方程y″＝Pm（x）两端积分两次得到.

例5　求方程y″＋4y′＋2y＝x－1的一个特解.

解　由于右端f（x）＝P1（x）＝x－1，q＝2≠0，故可设特解为

类型2　f（x）＝Pm（x）·eλx，其中Pm（x）为m次多项式.

此时可设特解的试解函数为

其中Qm（x）是与Pm（x）同次的多项式，即

k的取值方法如下：

当λ不是特征根时，k＝0；

当λ是特征单根时，k＝1；

当λ是特征重根时，k＝2.

类型1是类型2的特例，可看作λ＝0时的情形.

例6　求方程y″＋4y′＋2y＝ex的一个特解.

解　由于λ＝1不是特征根，Pm（x）＝1，故可设特解为

代入原方程，得

所以A＝，故所求方程的特解为

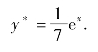
类型3　f（x）＝a1cosωx＋a2sinωx，这里，a1，a2，ω为常数.

此时可设特解为

其中A1，A2为待定系数，且当±iω为特征方程的根时，取k＝1；当±iω不是特征方程的根时，k＝0.

例7　求方程y″＋2y′＋3y＝2sinx的特解的形式.

解　所给方程对应的齐次方程的特征方程为

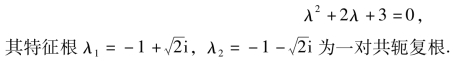
显然，±i不是特征方程的根，故k＝0，所以该方程的特解的形式为

类型4　f（x）＝eαx（a1cosωx＋a2sinωx），这里，a1，a2，ω为实常数.

此时可设特解为

其中A1，A2为待定系数，且当α±iω为特征方程的根时，取k＝1；当α±iω不是特征方程的根时，k＝0.

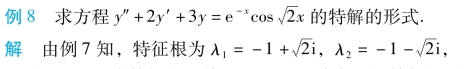
显然，α±iω为特征根，故k＝1，所以该方程的特解的形式为