【摘要】:讨论幂级数的性质,指的是幂级数的和函数S(x)的性质.同一般函数类似,幂级数也有加减乘、微分与积分等运算性质.在求解具体问题时,这些运算性质起着十分重要的作用.下面以幂级数(9.3)为例,介绍幂级数的四则运算性质及其和函数的分析性质.1.幂级数的四则运算性质设幂级数与的收敛半径分别为R1和R2,记R=min{R1,R2},其和函数分别为S1(x)和S2(x),那么对于收敛的幂级数有如下的四则运算性
讨论幂级数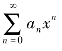 的性质,指的是幂级数的和函数S(x)的性质.同一般函数类似,幂级数也有加减乘、微分与积分等运算性质.在求解具体问题时,这些运算性质起着十分重要的作用.
的性质,指的是幂级数的和函数S(x)的性质.同一般函数类似,幂级数也有加减乘、微分与积分等运算性质.在求解具体问题时,这些运算性质起着十分重要的作用.
下面以幂级数(9.3)为例,介绍幂级数的四则运算性质及其和函数的分析性质.
1.幂级数的四则运算性质
设幂级数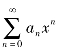 与
与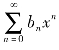 的收敛半径分别为R1和R2,记R=min{R1,R2},其和函数分别为S1(x)和S2(x),那么对于收敛的幂级数有如下的四则运算性质:
的收敛半径分别为R1和R2,记R=min{R1,R2},其和函数分别为S1(x)和S2(x),那么对于收敛的幂级数有如下的四则运算性质:
2.幂级数的和函数的分析性质
注:此性质说明极限符号可以和无限求和符号交换次序.
(2)逐项可导性:S(x)在收敛区间(-R,R)内可导,并且可以逐项求导,即
注:此性质说明求导符号可以和无限求和符号交换次序.(https://www.daowen.com)
(3)逐项可积性:S(x)在收敛区间(-R,R)内可积,并且可以逐项求积分,即
注:此性质说明积分符号可以和无限求和符号交换次序.
需要注意的是,将幂级数逐项求导或逐项积分后,所得到的新的幂级数的收敛半径不会改变,但是收敛区间的两个端点的敛散性将会变化,需另外加以判别.
利用一些已知幂级数的和函数以及幂级数的基本性质,可以求出某些幂级数的和函数,如,
习题 9.4
1.求下列幂级数的收敛半径、收敛区间和收敛域.
2.求下列幂级数的和函数.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






