在初等数学中遇到的加法，都是有限项的和式，但在某些实际问题中，会出现无穷多项相加的情形.

1.引例

我国古代数学理论的奠基者之一，魏晋时的数学家刘徽曾利用圆的内接正多边形来计算圆的面积，称为割圆术，其具体做法是，在半径为1的单位圆内作一内接正六边形，其面积记为a1，它可以作为圆面积A的一个近似值，再以正六边形每一条边为底，在小弓形内作一个顶点在圆周上的等腰三角形（如图9.1），记这六个三角形的面积之和为a2，于是圆内接正十二边形的面积之和为a1＋a2，a1＋a2较a1更接近圆的面积A.依次继续下去，可以得到一系列圆面积的近似值：

图9.1

A1＝a1，

A2＝a1＋a2，

……

An＝a1＋a2＋…＋an.

当n无限增大时，就得到一个由无穷多个数相加的式子a1＋a2＋…＋an＋…，这样的式子称为常数项无穷级数.

下面，我们引入无穷级数的定义.

2.级数的定义

定义1　设给定一个数列{u}n，把它的各项依次用加号连接起来的表达式(www.daowen.com)

显然，我们无法直接对无穷多个实数逐个地相加，所以必须对上述的级数求和给出合理的定义.这样，我们可以利用级数的部分和数列{S}n是否有极限来研究无穷多项相加的和是否存在，即级数是收敛还是发散的情况.

为调和级数，试证明该级数是发散的.

例2　称无穷级数

为几何级数（或等比级数），其中a≠0，试讨论该级数的敛散性.

解　我们已经知道，几何级数的前n项和

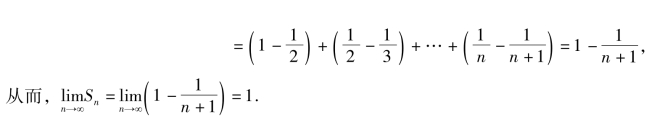
所以，该级数收敛于1．