当积分区域D是圆域、环域、扇形域等，或者被积函数为形如f（x2＋y2），等的形式时，在极坐标系下计算二重积分较为方便.

在平面上选定一点O，从点O出发引出一条射线Ox，并在射线上规定一个单位长度，这就得到了极坐标系，如图8.15所示，其中O称为极点，射线Ox称为极轴.

图8.15

对平面上的一点M，线段OM的长度称为点M的极径，记为r（或ρ），显然r≥0.以极轴为始边以线段OM位置为终边的角称为点M的极角，记为θ.这样平面上每一点M都可以用它的极径r和极角θ来确定其位置，称有序数组（r，θ）为点M的极坐标.

如图8.16所示，选取极坐标系时，若以平面直角坐标系的原点O为极点，以x轴为极轴，则直角坐标系中的两个坐标x和y与极坐标系中的两个坐标r和θ的关系为

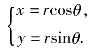
图8.16

在极坐标系下，我们用一簇圆心在极点的同心圆r＝常数（r≥0）及另一簇从极点出发的射线θ＝常数（0≤θ≤2π）将区域D分割成许多小区域，如图8.17所示.

图8.17

将极角分别为θ与θ＋Δθ的两条射线和半径分别为r与r＋Δr的两条圆弧所围成的小区域记作Δσ，则由扇形面积公式，得

当Δr和Δθ充分小时，我们略去高阶无穷小量得

此时，极坐标系中的面积元素为

故直角坐标系下的二重积分变换为极坐标系下的二重积分的公式为

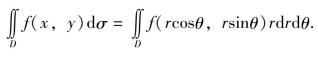
在极坐标系下计算二重积分，仍然需要化为二次积分来计算，通常是按先r后θ的顺序进行，下面分三种情况讨论.

（1）极点O在区域D之外，且D由射线θ＝α，θ＝β和连续曲线r＝r1（θ），r＝r2（θ）所围成，如图8.18所示，此时，D可以表示为

则有

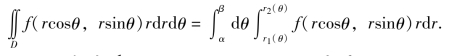
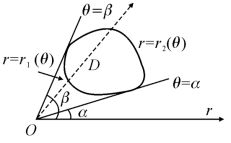
图8.18

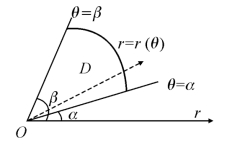
图8.19

（2）极点O在区域D的边界上，且D由射线θ＝α，θ＝β和连续曲线r＝r（θ）所围成，如图8.19所示，此时，D可以表示为

则有(www.daowen.com)

（3）极点O在区域D内部，且D的边界曲线为连续封闭曲线：r＝r（θ），如图8.20所示，此时，D可以表示为

则有

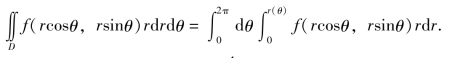
图8.20

例5　计算定积分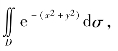其中D是由圆x2＋y2＝R2所围成的区域.

解　画出积分区域D的图形，如图8.21所示，在极坐标系下，积分区域可表示为

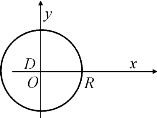
图8.21

则有

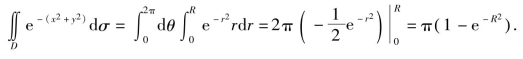
例6　计算定积分其中D是由圆x2＋y2＝2y所围成的区域.

解　画出积分区域D的图形，如图8.22所示，在极坐标系下，积分区域可表示为

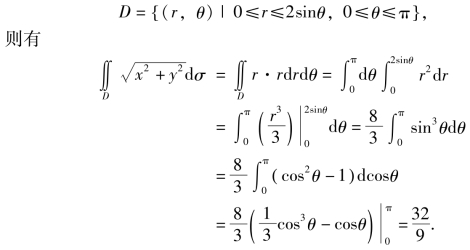
图8.22

例7　计算定积分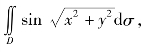其中区域D是π2≤x2＋y2≤4π2.

图8.23

解　画出积分区域D的图形，如图8.23所示.

在极坐标系下，积分区域可表示为

习题　8.2

1.计算下列二重积分.

2.交换下列二次积分的次序.

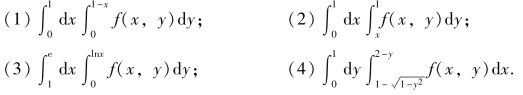
3.利用极坐标计算下列二重积分.