如果函数f（x，y）在有界区域D上连续，则f（x，y）在D上必定取得最大值和最小值，使函数取得最大值或最小值的点既可能在D内部，也有可能在D的边界上，如果函数f（x，y）在D内部的点（x0，y0）处取得最大值或最小值，则（x0，y0）必是函数的极值点.因此求f（x，y）在D上的最大值和最小值可采取下述方法：

（1）求出f（x，y）在D内的可能极值点（全部驻点、一阶偏导数不存在的点），并求出其函数值；

（2）求出f（x，y）在D的边界上的最大值和最小值（这是以函数f（x，y）为目标函数，以D的边界曲线方程为约束条件的条件极值问题）；

（3）比较上述函数值的大小，最大的就是函数f（x，y）在D上的最大值，最小的就是函数f（x，y）在D上的最小值.

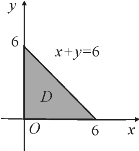
图7.30

例1　求函数f（x，y）＝x2（4y－xy）－x2y2在区域D上的最大值和最小值，其中D是由x＋y＝6、x＝0及y＝0所围成的闭区域.

解　区域D如图7.30所示.函数f（x，y）在闭区域D上连续，在D内可偏导.(www.daowen.com)

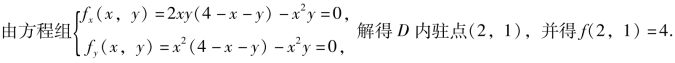
下面考虑f（x，y）在D的边界上的情况：

当x＝0，0≤y≤6时，f（x，y）＝0；当y＝0，0≤x≤6时，f（x，y）＝0；当x＋y＝0，0≤x≤6时，f（x，y）被限制在x＋y＝0上，所以f（x，y）可表示为一元函数

由h′（x）＝6x（x－4）＝0，得h（x）在（0，6）内唯一驻点x＝4，且h（4）＝f（4，2）＝－64，又h（0）＝h（6）＝0，可知h（x）在[0，]

6上的最大值为0，最小值是－64.

比较以上可得，f（x，y）在D上的最小值f（4，2）＝－64，最大值为f（2，1）＝4.