1.极值的定义

定义1　设函数都有z＝f（x，y）在点P0（x0，y0）的某一邻域U0（P0）内有定义，如果对任意（x，y）∈U。（P0），都有

成立，则称f（x0，y0）是f（x，y）的一个极大值（或极小值），极大值和极小值统称为极值；点（x0，y0）称为f（x，y）的极大值点（或极小值点），极大值点和极小值点统称为极值点.

例如，函数z＝在点（0，0）处取得极小值z（0，0）＝0，如图7.28所示.而函数z＝xy既取不得极大值也取不得极小值，因为在点（0，0）处的函数值为零，而在点（0，0）的任意邻域内，总有使函数值为正的点，也有使函数值为负的值，如图7.29所示.

图7.28

图7.29

对于可导的一元函数y＝f（x），我们知道在点x0处有极值的必要条件是f′（x0）＝0，对于多元函数我们也有类似的结论.

定理1（极值存在的必要条件）　设函数z＝f（x，y）在点（x0，y0）处具有偏导数，且在点（x0，y0）处取得极值，则有

证　不妨设z＝f（x，y）在点（x0，y0）处具有极大值，由极大值定义，在点（x0，y0）的某邻域内异于（x0，y0）的点（x，y）都满足不等式f（x，y）＜f（x0，y0）.

特殊地，在该邻域内取y＝y0，而x≠x0的点，也因有不等式f（x，y0）＜f（x0，y0），这表明一元函数z＝f（x0，y0）在x＝x0处取得极大值，所以必有fx（x0，y0）＝0，类似地可使fy（x0，y0）＝0.

定义2　使fx（x0，y0）＝0和fy（x0，y0）＝0同时成立的点（x0，y0）称为z＝f（x，y）的驻点.

由定理1可知，对可偏导函数f（x，y），极值点必为驻点，但函数的驻点不一定是极值点.例如，点（0，0）是函数z＝xy的驻点，但函数在该点并无极值.

另外，函数f（x，y）偏导数不存在的点也可能是它的极值点.例如，函数z＝在点（0，0）处取得极小值，但它的两个偏导数在点（0，0）处都不存在.

下面给出判别二元函数f（x，y）的驻点是否为极值点的充分条件.(www.daowen.com)

定理2（极值存在的充分条件）　设函数z＝f（x，y）在点（x0，y0）的某邻域内具有二阶连续偏导数，且（x0，y0）是f（x，y）的驻点，记

则f（x，y）在点（x0，y0）处是否取得极值的条件如下：

B2－AC＜0时具有极值，且当A＜0时具有极大值，当A＞0时具有极小值；

B2－AC＞0时没有极值；

B2－AC＝0时可能有极值，也可能没有极值，需另做讨论.

定理证明从略.

利用上面两个定理，对于具有二阶连续偏导数的函数z＝f（x，y），可有如下求极值的方法：

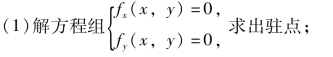
（2）对于每一个驻点（x0，y0），求出相应的二阶偏导数的值A，B，C；

（3）定出B2－AC的符号，按定理2的结论判断f（x0，y0）是否是极值，是极小值还是极大值.

例1　求函数f（x，y）＝x3－y3＋3x2＋3y2－9x的极值.

解　由方程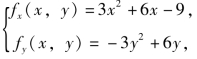求得驻点为（1，0），（1，2），（－3，0），（－3，2）；再求二阶偏导，得fxx（x，y）＝6x＋6，fxy（x，y）＝0，fyy（x，y）＝－6y＋6．

（1）在点（1，0）处，B2－AC＝－72＜0，且A＝12＞0，所以函数在点（1，0）处取得极小值f（1，0）＝－5；

（2）在点（1，2）处，B2－AC＝72＞0，所以f（1，2）不是极值；

（3）在点（－3，0）处，B2－AC＝72＞0，所以f（－3，0）也不是极值；

（4）在点（－3，2）处，B2－AC＝－72＜0．且A＝－12＜0，所以函数在点（－3，2）处取得极大值f（－3，2）＝31.