在一元函数微分学中,复合函数的求导法则起着重要的作用,现在我们把它推广到多元复合函数中.下面按照多元复合函数不同情形,分三种情况讨论.
1.复合函数中间变量均为一元函数的情形
定理1 如果函数u=φ(t),v=ψ(t)都在点t处可导,函数z=f(u,v)在对应点(u,v)处可微,则复合函数z=f[φ(t),ψ(t)]在点t处可导,且有

证 设t取得增量Δt,这时u=φ(t),v=ψ(t)的对应增量为Δu,Δv,函数z=f[φ(t),ψ(t)]相应的获得增量Δz.由于函数z=f[u,v]可微,所以有

这就证明了复合函数z=f[φ(t),ψ(t)]在点t处可导且公式成立.
公式中的变量之间的关系如图7.22所示:
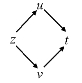
图7.22
其中,从引出的两个箭头指向u,v,表明函数z有两个中间变量u和v;而由u与v分别引出的一个箭头指向t,表明中间变量分别是t的函数.
上述定理中复合函数中间变量的情形可以推广到多于两个变量的情形.例如,设由函数u=f(x,y,z),x=φ(t),y=ψ(t),z=w(t)复合而得复合函数
![]()
变量之间的关系如图7.23所示:

图7.23
上述复合函数在点t亦可导,且有
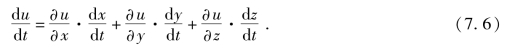
上述公式中的导数称为全导数.
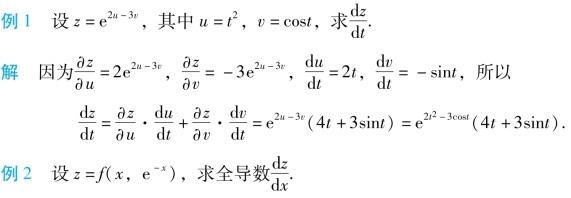
解 令y=e-x,则z=f(x,y),变量间的关系如图7.24所示,则
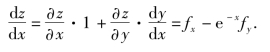
![]()
图7.24
2.复合函数的中间变量均为多元函数的情形
定理2 如果函数u=φ(x,y),v=ψ(x,y)都在点(x,y)处具有对x及对y的偏导数.函数z=f(u,v)在对应于(x,y)的点(u,v)处可微,则复合函数z=f(φ(x,y),ψ(x,y))在点(x,y)处的两个偏导数存在,且有
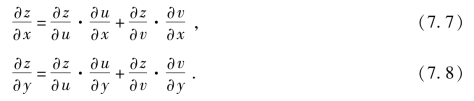
变量之间的关系如图7.25所示.
 (https://www.daowen.com)
(https://www.daowen.com)
图7.25
事实上,求![]() 时,将y看作常量,因此中间变量u即v仍可看作x一元函数,这样问题就转化为定理1的情形.类似的可得
时,将y看作常量,因此中间变量u即v仍可看作x一元函数,这样问题就转化为定理1的情形.类似的可得![]() 上式称为求复合函数偏导的链式法则.
上式称为求复合函数偏导的链式法则.
对于情况更复杂的复合函数也有类似的结果.例如,设u=φ(x,y),v=ψ(x,y)及w=ω(x,y)均在点(x,y)处具有对x及y的偏导数,而函数z=f(u,v,w)在对应点(u,v,w)处可微,则复合函数z=f(φ(x,y),ψ(x,y),ω(x,y))在点(x,y)处的两个偏导数都存在,变量关系如图7.26所示.
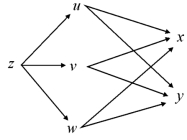
图7.26
在与定理2相似的条件下有:

3.复合函数的中间变量既有一元函数,又有多元函数的情形
定理3 如果函数u=φ(x,y)在点(x,y)处具有对x及对y的偏导数,v=φ(y)在点y处可导,函数z=f(u,v)在对应于(x,y)的点(u,v)处可微,则复合函数z=f(φ(x,y),φ(y))在点(x,y)处偏导数存在,且有
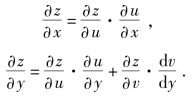

图7.27
变量之间的关系如图7.27所示.
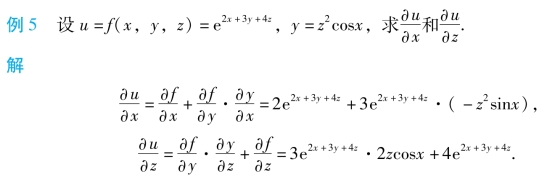
4.全微分形式不变性
定理4 如果函数z=f(u,v)在点(u,v)处可微,函数u=φ(x,y)及v=ψ(x,y)都在对应点(x,y)处可微,则不论u,v作为函数z=f(u,v)的自变量,还是作为复合函数z=f(φ(x,y),ψ(x,y))的中间变量,都有
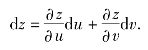
证 如果z作为u,v为自变量的函数,根据全微分的计算公式,有
![]()
如果z作为u,v为中间变量的复合函数,则由复合函数的求导法则有
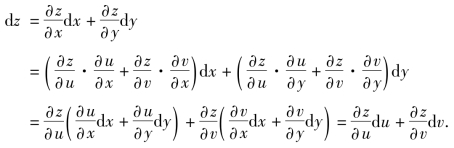
因此无论u,v是自变量还是中间变量,函数的全微分都可写成相同的形式,这个性质称为全微分的形式不变性.
例6 利用全微分的形式不变性解本节的例3.
解 因为dz=duv=vuv-1du+uvlnudv,而
![]()
则dz=duv=vuv-12(xdx+ydy)+uvlnu(ydx+xdy)
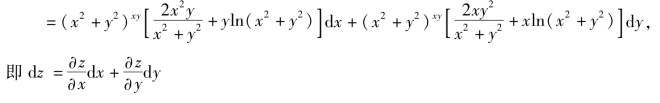

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





