定理1（可微的必要条件）　如果函数z＝f（x，y）在点（x0，y0）可微，则

（1）函数z＝f（x，y）在点（x0，y0）处连续；

（2）函数z＝f（x，y）在点（x0，y0）处可偏导，且有A＝fx（x0，y0），B＝fy（x0，y0）.

证　因函数z＝f（x，y）在点（x0，y0）处可微，则

（1）在上式中令Δx→0，Δy→0，有

即函数z＝f（x，y）在点（x0，y0）处连续.

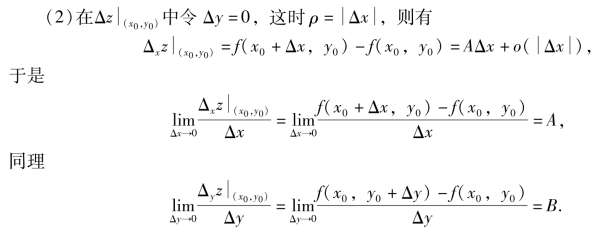
即函数z＝f（x，y）在点（x0，y0）处可偏导，且有A＝fx（x0，y0），B＝fy（x0，y0）.

可见，如果函数z＝f（x，y）在点（x0，y0）可微，则有函数z＝f（x，y）在点（x0，y0）的全微分为

当函数z＝f（x，y）在区域D内每一点都可微时，称z＝f（x，y）为D内的可微函数，此时，函数z＝f（x，y）的微分可表示为

注　多元函数在一点处可偏导只是它在该点可微的必要条件，但不是充分条件.

例如：函数

(www.daowen.com)

定理2（可微的充分条件）　如果函数z＝f（x，y）在点P0（x0，y0）处的某邻域U（P0）内可偏导，且偏导数fx（x，y），fy（x，y）都在点（x0，y0）处连续，则函数f（x，y）在点（x0，y0）处可微分.

综上所述，二元函数的可微、偏导数及连续之间有如图7.21所示的关系.

图7.21

定理1和定理2的结论可推广到三元及三元以上函数.

与一元函数的微分相似，可以得到自变量的微分就是自变量的增量，即dx＝Δx，dy＝Δy.于是函数z＝f（x，y）在点P（x，y）的全微分为

类似地，三元函数u＝f（x，y，z）的全微分为

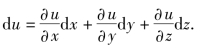
例1　计算函数z＝在点（1，2）处当Δx＝0.1，Δy＝－0.2时的全微分与全增量.

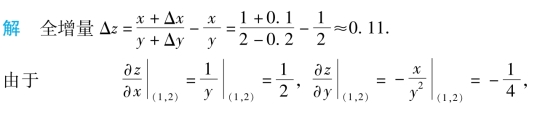
所以

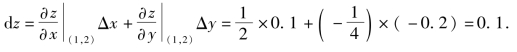
例2　计算函数z＝x2y＋tan（x＋y）的全微分.

解　因为