【摘要】:引例1金属薄片受热膨胀问题.如图7.20所示的一长方形金属薄片,其长和宽分别为x和y,则面积为S=xy.当受热后在长和宽两个方向上都发生变形,受热变形后的长和宽分别为x+Δx和y+Δy,那么该金属薄片的面积就有如下全增量上式右端包含两个部分,一部分是yΔx+xΔy,它是Δx,Δy的线性函数;另一部分是ΔxΔy,当Δx→0,Δy→0时,即当ρ=→0时,ΔxΔy是比ρ高阶的无穷小量.因此,如果略去Δ

引例1 金属薄片受热膨胀问题.
如图7.20所示的一长方形金属薄片,其长和宽分别为x和y,则面积为S=xy.当受热后在长和宽两个方向上都发生变形,受热变形后的长和宽分别为x+Δx和y+Δy,那么该金属薄片的面积就有如下全增量
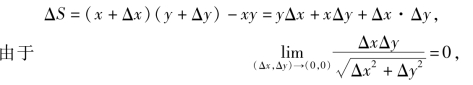
上式右端包含两个部分,一部分是yΔx+xΔy,它是Δx,Δy的线性函数;另一部分是ΔxΔy,当Δx→0,Δy→0时,即当ρ=![]() →0时,ΔxΔy是比ρ高阶的无穷小量.因此,如果略去ΔxΔy,用yΔx+xΔy近似表示ΔS,则其误差ΔxΔy是一个比ρ高阶的无穷小量.以后一般把这个线性函数yΔx+xΔy称为函数S=xy在点(x,y)的全微分,面积S的改变量ΔS称为面积函数的全增量.
→0时,ΔxΔy是比ρ高阶的无穷小量.因此,如果略去ΔxΔy,用yΔx+xΔy近似表示ΔS,则其误差ΔxΔy是一个比ρ高阶的无穷小量.以后一般把这个线性函数yΔx+xΔy称为函数S=xy在点(x,y)的全微分,面积S的改变量ΔS称为面积函数的全增量.
一般地,计算函数z=f(x,y)的全增量Δz比较复杂.与一元函数类似,希望能用Δx和Δy的线性函数近似代替函数z的全增量,从而引入全微分的概念.
定义1 设二元函数z=f(x,y)在点P0(x0,y0)处的某邻域U(P0)内有定义,若函数在P0(x0,y0)处的全增量
![]()
可表示为(www.daowen.com)
![]()
其中A、B仅与x0,y0有关,而与Δx,Δy无关,ρ=![]() ,o(ρ)表示关于ρ的高阶无穷小量,则称函数z=f(x,y)在点(x,y)可微,并称AΔx+BΔy为f(x,y)在点(x0,y0)的全微分,记为
,o(ρ)表示关于ρ的高阶无穷小量,则称函数z=f(x,y)在点(x,y)可微,并称AΔx+BΔy为f(x,y)在点(x0,y0)的全微分,记为![]() ,即
,即
![]()
由于自变量的增量等于自变量的微分,即
![]()
于是
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关经济数学(微积分)的文章






