在一元函数微分学中，我们引入边际与弹性的概念来分别表示经济函数在一点的变化率与相对变化率，这些概念推广到多元函数微分学中，并被赋予了更丰富的经济含义.

1.边际分析

一元函数的导数在经济学中称为边际函数，同样地，n元函数f（x1，x2，…，xn）关于x的偏导函数fxi（x1，x2，…，xn）称为f关于xi（i＝1，2，…，n）的边际函数，其在一点P0的值f（P0）称为边际函数值，以n＝2为例，称

为f（x，y）在点（x0，y0）处对x的边际函数值.

边际函数值的含义是：在P0处，仅当改变其中一个自变量xi（i＝1，2，…，n）一个单位，而其余n－1个自变量保持不变时，函数f（x1，x2，…，xn）近似改变了fxi（x1，x2，个单位.

（1）联合成本函数的边际分析

设某厂商生产A，B两种产品，当A产品的产量为QA个单位，B产品的产量为QB个单位时，总成本为C＝f（QA，QB），这里的C＝f（QA，QB）称为联合成本函数，偏导的经济意义是：当B产品的产量固定为QB时，A产品的产量在QA的基础上再生产一个单位时成本大约增加元.

例9　某厂生产I型和Ⅱ两种型号的电视机，其成本函数为

其中Q1，Q2分别表示I型和Ⅱ两种型号的电视机的产量（单位：台），厂商为I型和Ⅱ两种型号的电视机的定价分别为2000元／台和8000元／台，假设生产的产品全部能够售出，当生产I型电视机300台和Ⅱ型电视机50台时，求边际成本，并解释其经济意义.

此结果表明，在Ⅱ型电视机的产量保持50台不变的情形下，厂商在生产300台的基础上再生产一台Ⅰ型电视机需要追加的成本为1300元，而在Ⅰ型电视机的产量保持300台不变的情形下，厂商在生产50台的基础上再生产一台Ⅱ型电视机需要追加的成本为6300元.

（2）需求函数的边际分析

假设A，B两种商品是彼此相关（商品之间的相关关系可以分为两种，一种为替代关系，即两种商品之间可以互相代替以满足消费者的某一愿望，这两种商品互为替代品；另一种为互补关系，即两种商品必须同时使用才能满足消费者的某一愿望，这两种商品互为互补品）的，那么A与B的需求量QA，QB都是两种商品的价格PA，PB及消费者的收入y的函数，即

可以求得如下6个偏导数：

其称为商品A的需求函数关于PA的边际需求，它表示当商品B的价格PB和消费者的收入y固定时，商品A的价格变化一个单位时商品A的需求量的近似增称为商品A的需求函数关于收入y的边际需求，它表示当PA，PB固定时，消费者的收入变化一个单位时商品A的需求量的近似增量.同理可得其他偏导数的经济意义.

如果PB，y固定而PA上升时，商品A的需求量QA将减少，＜0；同理可＜0，当PA，PB固定而消费者的收入y增加时，一般地，QA将增大，从而有＞0；同理可如＞0和＞0，则称A，B两种商品称为替代品，例如苹果和香蕉就是替代品，如＜0和＜0，则称A，B两种商品为互补品，例如汽车和汽油就是互补品.

例10　设A，B两种商品是彼此相关的，它们的需求函数分别为

试确定A，B两种商品的关系.

解　由于函数中不含有收入y，则可求出四个偏导数：

因为PA＞0，PB＞0，所以

这就说明了A，B两种商品为替代品.

2.偏弹性分析

在经济学理论中，特别是在计量经济学中，经常应用弹性的概念来定量分析各经济变量之间的变动关系，一般来说，只要两个经济变量之间存在着函数关系，我们就可以用弹性来表示因变量对自变量变化的反应关系灵敏程度，直观地讲就是，当一个经济量发生1%的变动的百分比.

偏弹性是一元函数的弹性概念在多元函数情形的推广，它是多元函数关于某个自变量的相对变化率.

称为函数f（x，y）在点（x0，y0）处对x从x0到x0＋Δx两点间的弹性，当Δx→0时，这个比值的极限称为函数f（x，y）在点（x0，y0）处对x的相对变化率，即相对导数，或相对函数，或称为偏弹性，记作即

当x0较大而Δx较小时，我们有

其含义是：反映函数f（x，y）在点（x0，y0）处随x的变化，其变化幅度的大小，或f（x，y）在点（x0，y0）处对x变化反应的强烈程度或灵敏度，具体地说表示在（x0，y0）处，当y不变而x改变1%时，z＝f（x，y）近似地改变εx%.

可类似地定义f（x，y）在点（x0，y0）处对y的偏弹性

由偏弹性的定义可知，偏弹性是无量纲的，下面以需求函数为例来介绍偏弹性的经济意义.

一种商品的价格常常受多种因素的影响，相关商品的价格也是其中一个重要的因素，假设其他因素不变，仅仅研究一种商品的需求量变化与相关商品的价格变化之间的关系，就需要应用需求的交叉价格弹性.

由上式知对于A，B两种商品，其需求函数分别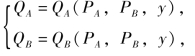当PA和y保持不变而PB发生变化时，称偏弹性(www.daowen.com)

为A商品的需求QA对PB交叉弹性，可类似定义B的商品的需求QB对PA的交叉弹性为

需求的交叉价格弹性表示一定时期内当所有其他变量保持不变时，该种商品的需求量的变动对于他的相关商品价格变动反应的灵敏度.

A商品的需求QA对B商品的价格PB的交叉弹性εPB可正可负，也可能为零，要取决于两种商品的相关关系，一般来说：

（1）若B商品是A商品的替代品，则A商品的需求量和它的替代品的价格PB之间呈同方向的变动，此时

（2）若B商品是A商品的互补品，则A商品的需求量和它的互补品的价格PB之间呈反方向的变动，此时

（3）若B商品既不是A商品的替代品，也不是A商品的互补品，而是无关品，则A商品的需求量对B商品的价格PB的变动不会做出反应，此时

对替代品而言，两种商品之间的可替代程度越大，交叉弹性越大；对互补品而言，两种商品的互补性越强，交叉弹性的绝对值越小，反过来，我们也可以根据两种商品之间需求的交叉价格弹性系数的符号来判断它们之间的相关关系.

我们在前面考查的弹性都是就商品的供给数量与商品的价格之间的关系进行研究的，实际上弹性关系并不局限与商品的供给数量和商品的价格之间，而是被广泛地应用于各种相关的经济变量之间.

例如，上式中商品A需求的收入弹性为

它就是建立在消费者的收入和商品的需求量之间的关系基础上的一个弹性概念，它表示一定时期内当所有其他量保持不变时，该种商品的需求量的变动对于消费者收入变动反应的灵敏度.

根据商品需求的收入弹性系数值，商品可分为两类：

（1）若εy＞0，商品是正常品，正常品的需求量和消费者的收入之间呈同方向的变动；

（2）若εy＜0，商品是劣等品，劣等品的需求量和消费者的收入之间呈反方向的变动.

除了上述在西方经济学文献中经常出现的弹性概念外，根据所研究的具体经济问题的不同需要，经济学家们也经常建立一些新的弹性关系，在此就不赘述了.

例11　某种数码相机的销售量Q除与它自身的价格x（单位：百元）有关系外，还与配套的储存卡的价格y（单位：百元）有关，具体的关系式为

求当x＝25，y＝1时，

（1）销售量Q对x的弹性；

（2）销售量Q对y的交叉价格弹性；

（3）若储存卡的价格上涨5%，数码相机的销售量的变化率.

解　（1）销售量Q对x的弹性为

则当x＝25，y＝1时，

（2）销售量Q对y的交叉价格弹性为

则当x＝25，y＝1时，有

即数码相机的销售量下降56.5%.

习题　7.3

1.求下列函数在所给点处的偏导数.

2.求下列函数的偏导数.

7.f（x，y，z）＝xy2＋yz2＋x2z，求fx（0，0，1），fy（0，1，0），fxx（0，0，1），fxz（1，0，2），fyz（0，－1，0）和fzzx（2，0，1）.