1.偏导数的定义

在研究一元函数时，我们看到了函数对于自变量的变化率（即导数）的重要性，对于二元函数z＝f（x，y），同样需要研究它的变化率.

引例　设P为价格，L为广告费，则销售函数为Q＝APαLβ（A，α，β为常数），当考虑价格P不变时，销售量Q相对于广告费L的变化率时，可将看作L的一元函数，则Q′L＝βAPαLβ－1；类似地，考虑广告费L不变时，销售量Q对于价格P的变化率，将Q看成是P的函数，则有Q′P＝αAPα－1Lβ，这就是下面要研究的偏导数问题.

定义1　设函数z＝f（x，y）在点P0（x0，y0）的某邻域U（P0）内有定义，当自变量y固定在y0，而自变量x在x0处有增量Δx（Δx≠0）时，相应地函数有偏增量

如果极限

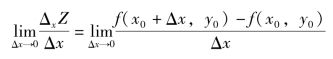
存在，则称此极限值为函数z＝f（x，y）在点（x0，y0）处关于自变量x的偏导数，

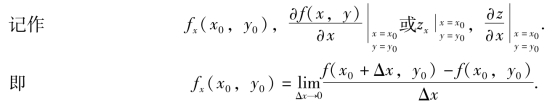
类似地，函数z＝f（x，y）在点（x0，y0）处关于自变量y的偏导数定义为

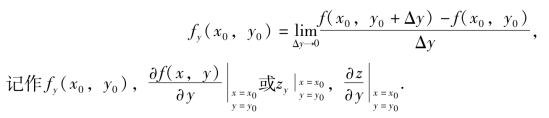
令x＝x0＋Δx，当Δx→0时，x→x0，故函数z＝f（x，y）在点（x0，y0）处关于自变量x的偏导数还可写成

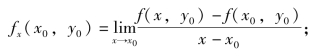
同理函数z＝f（x，y）在点（x0，y0）处关于自变量y的偏导数还可写成

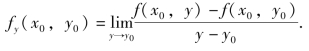
当函数z＝f（x，y）在点P0（x0，y0）处关于自变量x和y的偏导数都存在时，则称函数z＝f（x，y）在点P0（x0，y0）处可偏导.

如果函数z＝f（x，y）在区域D内每一点（x，y）处都可偏导，此时偏导数仍然是x和y的二元函数，就称它们为函数z＝f（x，y）的偏导函数，简称为偏导数.分别记作

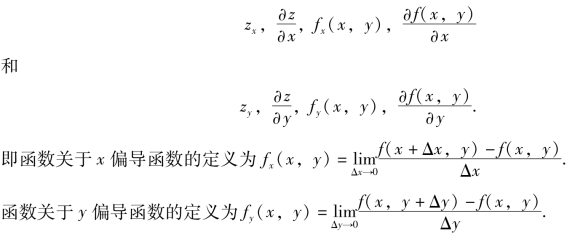
偏导数的概念还可推广到二元以上的函数.例如三元函数u＝f（x，y，z）在点（x，y，z）处对x的偏导数定义为

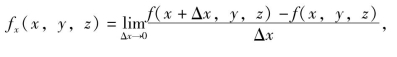
其中（x，y，z）是函数u＝f（x，y，z）的定义域内的点.它们的求法也仍然是一元函数的微分法问题.

2.偏导数的计算

由偏导数的定义可知，求二元函数z＝f（x，y）的偏导数，并不需要新的方法，如在求时，只要把y看作常量而对x求导数；求时，只要把x看作常量而对y求导数.

例1　求z＝x3－3xy2＋2y4在点（2，1）处的偏导数.

解　将y看作常数，对x求导数，

将x看作常数，对y求导数，得

于是，在点（2，1）处的偏导数为

(www.daowen.com)

例2　求z＝（x2＋y2）exy的偏导数.

解　z是x，y的二元函数.把y看作常数，对x求导数，得

把x看作常数，对y求导数，得

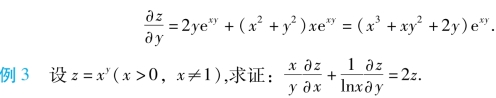
证　z对x，y的偏导数分别为

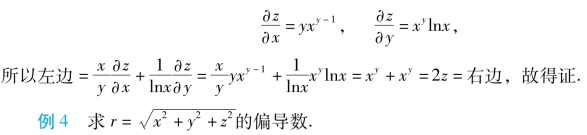
解　r是x，y，z的三元函数，把y和z都看作常数，得

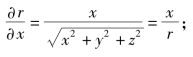
同理可得

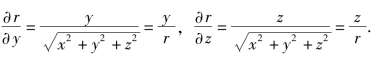
注　偏导数的记号是一个整体记号，不能理解为分子与分母之商，单独的∂z，∂x和∂y均无意义，这是与一元函数导数记号的不同之处.

例5　已知柯布－道格拉斯（Gobb－Douglus）生产函数Q＝ALαKβ（A，α，β均为正数），求产量Q关于劳动力L的边际产量，产量Q关于资金K的边际产量.

解　求产量Q关于劳动力L的边际产量，即将K看作常量，对L求导，得

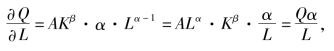
产量Q关于资金K的边际产量，即将L看作常量，对K求导，得

3.偏导数的几何意义

一元函数y＝f（x）的导数f′（x）的几何意义是曲线y＝f（x）在点（x0，y0）处切线的斜率，二元函数z＝f（x，y）的偏导数的几何意义也是曲线切线的斜率.

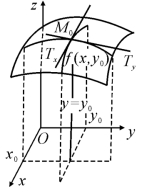
图7.19

即空间曲面z＝f（x，y）与平面x＝x0的交线z＝f（x0，y）在点P0（x0，y0，f（x0，y0））处的切线斜率.

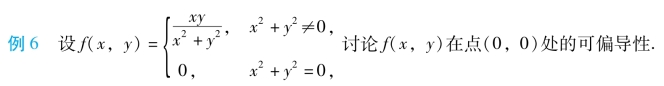
解　由偏导数的定义可知，

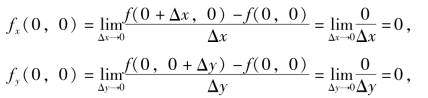
从而可知函数f（x，y）在点（0，0）处可偏导的.然而，由第2节例5知极不存在，从而函数f（x，y）在点（0，0）处不连续.