引例1　设本金p为常数，利息率为r，经过n个周期后，按复利计算的本利和为F＝p（1＋r）n，F随着变量r、n的变化而变化.

引例2　圆柱体的体积V和它的底半径r、高h之间具有关系V＝πr2h，这里，当r，h在集合{（r，h）｜r＞0，h ＞0}内取定一对值（r，h）时，V对应的值就随之确定.

1.二元函数的定义域

定义1　设非空点集D⊂R2，对于D中每一有序数组（x，y），变量z按照一对应法则f总有唯一确定的实数与之对应，则称z是变量x，y的二元函数，记为

区域D称为该函数的定义域，x，y称为自变量，z称为因变量.

二元函数z＝f（x，y）在点（x0，y0）处所取得的函数值，记为

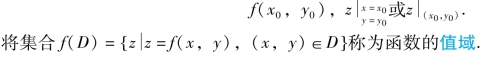
z是x，y的函数也可以记为z＝z（x，y），z＝φ（x，y）等等.

类似地，可以定义三元函数u＝f（x，y，z）以及三元以上的函数.通常把二元及二元以上的函数统称为多元函数.

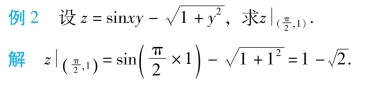
2.二元函数定义域

二元函数的定义域通常是一个平面区域，与一元函数的定义域类似，当自变量和因变量具有某种实际意义时，一般以自变量的实际意义来确定函数的定义域；当函数仅由解析式表示，则定义域就是使该解析式有意义的点（x，y）的全体构成的平面点集.

例3　求函数z＝ln（y－x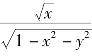）＋的定义域.

解　由函数的表达式可以看出，自变量的取值必须满足下列不等式组(www.daowen.com)

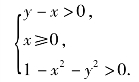
故函数的定义域为｛（x，y）｜y－x＞0，x≥0，x2＋y2＜1｝.它是平面上的一个有界开区域（如图7.15）.

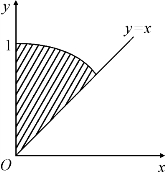
图7.15

图7.16

3.二元函数的几何意义

设函数z＝f（x，y）的定义域为坐标平面上的某个区域D，对于D中的任一点P（x，y）就有一个确定的实数z＝f（x，y）与之对应，于是得到空间直角坐标系中的一点M（x，y，z），当P点在区域D中变动时，相应的点M就在空间变动；当P点取遍中D的所有点时，点M的轨迹一般来说是空间的一个曲面（如图7.17）.这个曲面就是二元函数z＝f（x，y）的图形.即二元函数的几何图形一般为空间直角坐标系中的一个曲面，而其定义域D恰好是这个曲面在坐标平面xOy上的投影，因此也把z＝f（x，y）称为曲面方程.

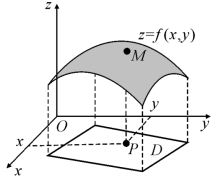
图7.17

例如：二元函数的图形是原点在中心，半径为1的上半球面，定义域是xOy平面上的以原点为中心的单位圆.（如图7.18）

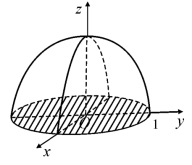
图7.18