由平面解析几何知道，当在平面上引入了一个直角坐标系后，平面上的点P与有序二元实数组（x，y）之间就建立了一一对应的关系.于是，人们常把有序实数组（x，y）与平面上的点P视作是等同的.这种建立了坐标系的平面称为坐标平面.坐标平面上具有某种性质P的点的集合，称为平面点集，记作

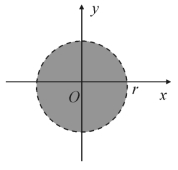
图7.12

例1　如图7.12所示，平面上以原点为中心、r为半径的圆内所有点的集合是

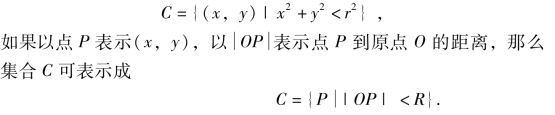
1.n维空间

我们知道平面直角坐标系中，平面上的点与二元有序数组（x，y）一一对应，二元有序数组（x，y）的全体所构成的集合称为二维空间，记作R2.在空间直角坐标系中，空间的点与三元有序实数组（x，y，z）一一对应，三元有序数组（x，y，z）的全体表示了空间中一切点的集合，我们用R3表示三元有序数组（x，y，z）全体构成的集合.

一般地，由n元有序实数组（x1，x2，…，xn）的全体构成的集合称为n维空间，记作Rn，即

其中每个有序数组（x1，x2，…，xn）称为Rn中的一个点，数xi称为该点的第i个坐标.类似地，n维空间中任两点P（x1，x2，…，xn）与Q（y1，y2，…，yn）间的距离定义为

2.点P0的δ邻域

设P0（x0，y0）是xOy平面上的一个点，δ是某一正数，与点P0（x0，y0）距离小于δ的点P（x，y）的全体，称为点P0的δ邻域，记为U（P0，δ），即

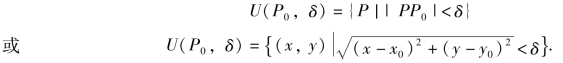
其中点P0（x0，y0）称为邻域的中心，δ称为邻域的半径.U（P0，δ）在几何上表示xOy平面内以点P0（x0，y0）为中心、δ（＞0）为半径的圆的内部点P（x，y）的全体.

当U（P0，δ）内不包含中心点P0时，则称此邻域为点P0的去心δ邻域，记作U。（P0，δ），即(www.daowen.com)

另外，如果不需要强调邻域的半径δ，则用U（P0）表示点P0的某个邻域，点P0的去心邻域记作

3.平面区域

我们可以利用邻域来描述点与点集之间的关系，设P为平面上任意点，E是一平面点集，则P与E有以下三种关系，

（1）若存在δ＞0，使得U（P，δ）⊂E，则称点P是E的内点.

（2）若存在δ＞0，使得U（P，δ）内不含有E的任何点，则称点P为E的外点.

（3）若在点P的任意邻域内，既含有属于E的点，又含有不属于E的点，则称点P为E的边界点.E的所有边界点的集合称为E的边界，记为∂E.

例如，点集E＝｛（x，y）≤x2＋y2＜9｝，满足1＜x2＋y2＜9的点都是E的内点；满足x2＋y2＝1的点均为E的边界点，它们都属于E；满足x2＋y2＝9的点也均为E的边界点，但它们都不属于E.E的边界是x2＋y2＝1和x2＋y2＝9.

若E的每一点都是它的内点，则称E为开集.

由xOy面上的一条或几条曲线所围成的一部分平面或整个平面，称为平面区域，简称区域.包括边界的区域称为闭区域；不包括边界的区域称为开区域.

如果存在常数M＞0，使得E⊂U（O，M），则称E为有界区域，否则称为无界区域.其中U（O，M）表示以原点O（0，0）为中心，M为半径的邻域.

平面图上的区域可用含该区域内的点的坐标的二元不等式或不等式组来表示，例如：

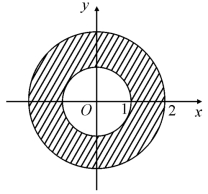
图7.13

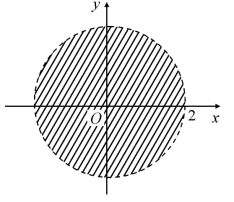
图7.14