1.曲面及其方程
类似于平面解析几何中的曲线一样,在空间解析几何中将曲面看作具有某种几何性质的动点的轨迹,用动点坐标(x,y,z)满足的方程来表示.
定义1 如果曲面S与三元方程
![]()
满足条件:
(1)曲面S上任意一点的坐标都满足方程(7.2);
(2)不在曲面S上的点的坐标都不满足方程(7.2),
那么,方程(7.2)就叫作曲面S的方程,而曲面S就叫作方程的图形(如图7.5).

图7.5
例3 设M(3,1,1),N(-1,0,2)是空间两点,求线段MN的垂直平分面的方程.
解 设点P(x,y,z)是所求平面上的任意一点,由题意有|PM|=|PN|,则
![]()
化简整理,得线段MN的垂直平分面的方程为
![]()
此方程是一个含有三个未知数的三元一次方程,表示一个垂直且平分线段AB的平面.
一般地,含有三个未知数的三元一次方程Ax+By+Cz+D=0(其中A,B,C,D都是常数,且A、B、C不同时为零)表示空间的一个平面.
例4 求球心为P0(x0,y0,z0),半径为R(>0)的球面方程.
解 设P(x,y,z)为球面上的任意一点,由题意有
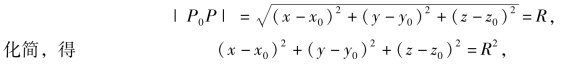
此方程即为球面的一般方程.
特别地,当球心在原点时,方程x2+y2+z2=R2为球心在原点,半径为R的球面方程.
2.二次曲面
与平面解析几何中规定的二次曲线相类似,把三元二次方程
![]()
所表示的空间曲面叫作二次曲面.其中Ai,Bi,Ci(i=1,2,3),D均为常数,且Ai,Bi,Ci(i=1,2,3)不全为零.(https://www.daowen.com)
常见的二次曲面除了球面外,还有:

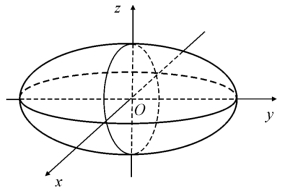
图7.6
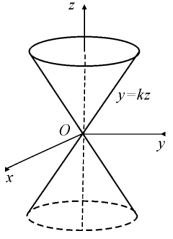
图7.7
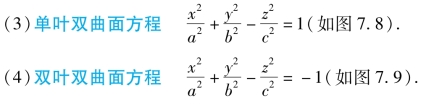
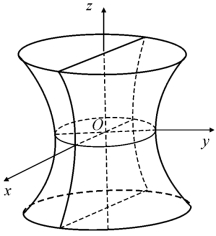
图7.8
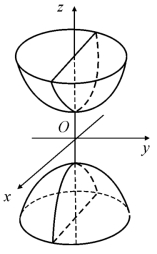
图7.9
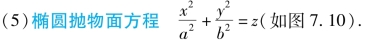
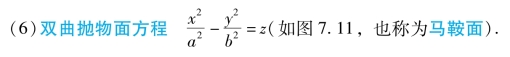
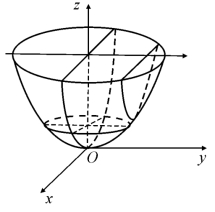
图7.10
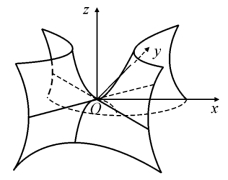
图7.11
习题 7.1
1.在空间直角坐标系下,指出下列各点的位置.
A(1,-3,-2);B(-2,1,-3);C(2,0,0);D(2,3,-1);E(2,3,0);F(1,2,3).
2.求在z轴上且与两点A(-4,1,7),B(3,5,-2)等距离的点.
3.求证以A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是一个等腰直角三角形.
4.求与两定点A(1,-2,0),B(2,0,-3)距离相等的点的轨迹方程.
5.做出下列方程所表示的空间图形.
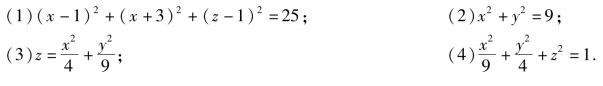
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







