过空间某一点O作三条两两相互垂直的数轴,它们都以O为原点且具有相同的长度单位,这三条数轴分别叫作x轴(横轴)、y轴(纵轴)、z轴(竖轴),统称为坐标轴,O称为坐标原点,它们构成一个空间直角坐标系O-xyz.这三条数轴的次序和正方向满足右手规则,即右手握住z轴,当右手的四个手指从x轴的正向![]() 角度转向y轴正向时,大拇指的指向就是z轴正向(如图7.1).
角度转向y轴正向时,大拇指的指向就是z轴正向(如图7.1).

图7.1
任意两个坐标轴可以确定一个平面,称为坐标平面.例如x轴及y轴所确定的坐标面叫作xOy平面,另两个坐标面是yOz平面和xOz平面.
三个坐标平面把空间分成八个部分,每一部分叫作卦限,含有三个正半轴的卦限叫作第一卦限,它位于xOy平面的上方.在xOy平面的上方,按逆时针方向排列着第二卦限、第三卦限和第四卦限.在xOy平面的下方,与第一卦限对应的是第五卦限,按逆时针方向还排列着第六卦限、第七卦限和第八卦限.八个卦限分别用字母Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ表示,如图7.2所示.
 (https://www.daowen.com)
(https://www.daowen.com)
图7.2
建立了空间直角坐标系,就可以建立空间的点与三个有序实数之间的对应关系.设M为空间中一已知点,过点M作三个平面分别垂直于x轴、y轴、z轴,这三个平面与三条坐标轴分别交于三点P、Q、R,如图7.3所示.设这三点在x轴、y轴、z轴上的坐标依次为x、y、z,这样空间中的一点M就唯一地确定了一个有序数组(x,y,z).反之对任一个三元有序数组(x,y,z),则可在x轴,y轴,z轴上分别取坐标为x,y,z的点P,Q,R,过点P,Q,R分别作平面与x轴,y轴,z轴垂直,这三个平面相交于一点M,则一个三元有序实数组就唯一地确定了空间的一点M.于是空间任意一点与一个三元有序数组建立了一一对应关系.有序数组(x,y,z)叫作M点的坐标,并依次称坐标x,y,z为点M的横坐标、纵坐标和竖坐标(或称点M的x坐标,y坐标,z坐标),记为M(x,y,z).

图7.3
显然,坐标原点O的坐标是(0,0,0),x轴上的点的坐标是(x,0,0),y轴上的点的坐标是(0,y,0),z轴上的点的坐标是(0,0,z),xOy平面上的点的坐标是(x,y,0),yOz平面上的点的坐标是(0,y,z),xOz平面上的点的坐标是(x,0,z).各个卦限中的点的坐标符号有如下规律:
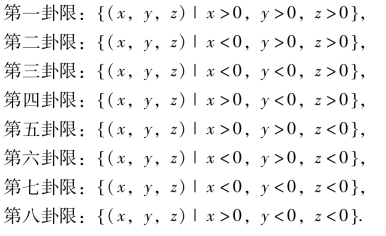
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






