1.平行截面面积已知的立体的体积

设某一空间立体介于垂直于x轴的两个平面x＝a与x＝b（a＜b）之间，其中平面x＝a是指过x轴上一点a且垂直于x轴的平面，用垂直于x轴的平面去截立体.若所得截面面积是关于x的已知连续函数S（x），如图6.11所示，则该立体的体积V也可用微元法求得.即用垂直于x轴的平面可以将立体V切成许多薄片，则立体的体积V就等于各薄片体积之和.

取x为积分变量，与区间上［a，b］任取一个小区间［x，x＋dx］相应的小薄片立体体积ΔV可近似地看作是底面积为S（x），高为dx的小直柱体的体积，即体积微元为

则所求立体的体积为

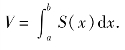
类似地，若某立体介于垂直于y轴的两个平面y＝c与y＝d（c＜d）之间，其中平面y＝c是指过y轴上点c且垂直于y轴的平面，该立体被垂直于y轴的平面所截，其截面面积S（y）是关于y的已知连续函数，如图6.12所示，则该立体的体积V为

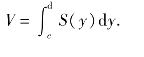
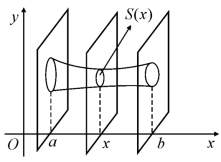
图6.11

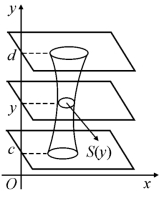
图6.12

例4　一平面经过半径为R的圆柱体的底圆中心，并与底面交成角α（图6.13），计算这个平面所截圆柱体所得部分立体的体积.

解　建立如图6.13所示的坐标系，则底圆的方程为x2＋y2＝R2，x的变化区间为［－R，R］.在［－R，R］上任取一点x，作与x轴垂直的平面，截得一直角三角形，它的两条直角边分别为y和ytanα，面积为

则所求立体的体积为

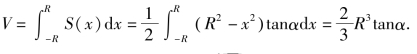
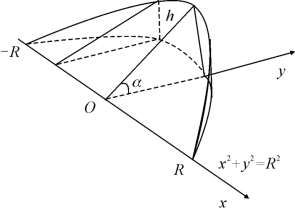
图6.13

2.旋转体的体积

旋转体是由一个平面图形绕这平面上的一条直线旋转一周所成的空间立体.称这条直线为旋转轴.下面我们用定积分的微元法来计算旋转体的体积.

求由连续曲线y＝f（x）（f（x）≥0）和直线x＝a，x＝b（a＜b）及y＝0所围成的平面图形，绕x轴旋转一周所成旋转体的体积Vx，如图6.14所示.

根据微元法，在区间［a，b］上任取一个小区间［x，x＋dx］，则这个小区间上的小曲边梯形绕轴旋转而成的小薄片体积就近似于底面积为πf2（x），高为dx的小直柱体的体积，即旋转体的体积微元dVx为(www.daowen.com)

则所求旋转体的体积为

类似地，由连续曲线x＝φ（y）（φ（y）≥0）以及直线y＝c，y＝d（c＜d），x＝0所围成的平面图形，绕y轴旋转一周所成旋转体的体积Vy（如图6.15）为

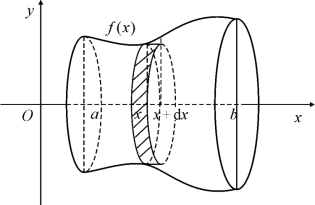
图6.14

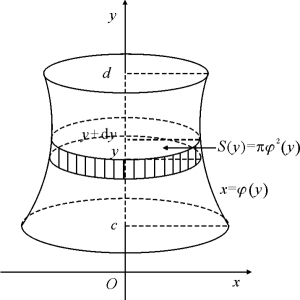
图6.15

例5　计算由椭圆曲线

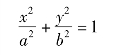
所围成的平面图形分别绕x轴和y轴旋转一周而成的旋转体（叫作旋转椭球体）的体积.

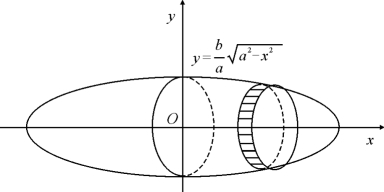
图6.16

解　由图6.16可见，如果旋转体看作是由上半个椭圆曲线与x轴所围成的平面图形绕x轴旋转一周而成的旋转体，则上半个椭圆曲线的方程为

选取x为积分变量，根据椭圆的对称性，绕x轴旋转的旋转体由式（6.1），得

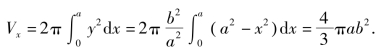
类似地，右半个椭圆曲线的方程为

绕y轴旋转的旋转体由式（6.2），得

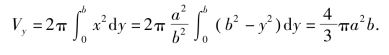
显然，当a＝b时，就是半径为a的球的体