设函数f（x）和g（x）在区间［a，b］上连续，求由曲线y＝f（x），y＝g（x）直线x＝a及x＝b所围成的平面图形的面积S（图6.6）.

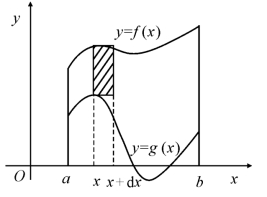
图6.6

特别地，由连续曲线y＝f（x）与直线x＝a，x＝b和x轴围成的图形的面积为

类似地，可以得到由曲线x＝φ（y），x＝φ（y）和直线y＝c，y＝d所围图形（如图6.7）的面积为

图6.7

图6.8

例1　求由y2＝x和y＝x2所围成的图形的面积.

解　画出图形（见图6.8），并由方程组

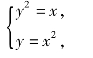
解得交点为（0，0）和（1，1）．

选x为积分变量，则x的变化范围为［0，1］，任取其上的一个区间［x，x＋dx］，则可得到相应于区间［x，x＋dx］的面积微元

故所求面积为

(www.daowen.com)

例2　求由y2＝2x和y＝x－4所围成的图形的面积.

解　画出图形（见图6.9），并由方程组

图6.9

解得它们的交点为（2，－2）和（8，4）.

选y为积分变量，则y的变化范围为［－2，4］，任取其上的一个区间［y，y＋dy］，则可得到相应于区间［y，y＋dy］的面积微元

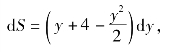
故所求面积为

例3　求在［0，2π］上由正弦曲线y＝sinx及x轴所围成图形的面积.

解　画出图形（见图6.10）.

图6.10

选x为积分变量，则x的变化范围为［0，2π］，任取其上的一个区间［x，x＋dx］⊂［0，π］，则可得到相应于区间［x，x＋dx］的面积微元

任取其上的一个区间［x，x＋dx］⊂［π，2π］，则可得到相应于区间［x，x＋dx］的面积微元

故所求面积为