为了进一步讨论定积分的理论和计算，本节将介绍定积分的一些性质.在下面的讨论中，我们总是假设函数在所讨论的区间上是可积的.

证明　先证a＜c＜b的情形，因为f（x）在区间［a，b］上可积，所以无论怎样划分［a，b］，积分和的极限都是存在的.因此我们在划分区间时，每次都选择c为分点，即

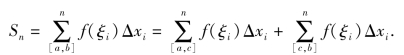
当λ→0时，对上式两端取极限，则有

再证a＜b＜c的情形，因为

同理可证，c＜a＜b的情形.从而无论a，b，c的相对位置如何，结论总是成立.

性质5（保号性）　若函数f（x）≥0，则

证明　因为f（x）≥0，故当a≤ξi≤b时，f（ξi）≥0.由定积分的定义有

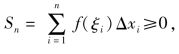
根据极限的保号性可得

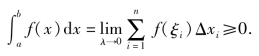
推论1（单调性）　若函数f（x）与g（x）在区间［a，b］上满足f（x）≥g（x），则

证明　由题设条件知f（x）－g（x）≥0，则由性质5有

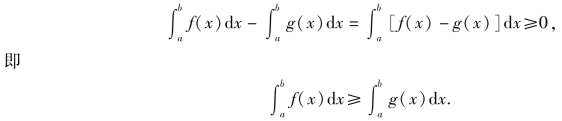
推论2　若函数｜f（x）｜在区间［a，b］上也可积，则有

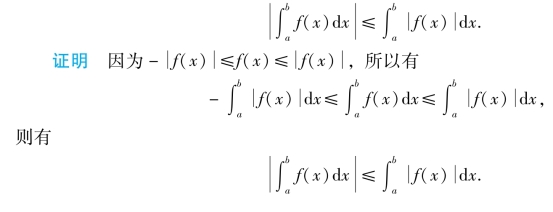
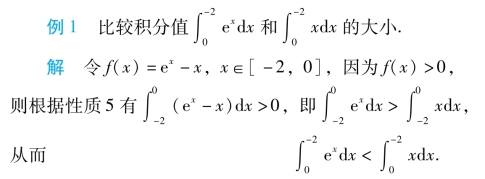
性质6（估值定理）　若M与m表示函数f（x）在区间［a，b］上的最大与最小值，则

证明　由已知有m≤f（x）≤M，根据性质5的推论1，得

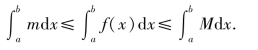
又由性质3和性质1，得(www.daowen.com)

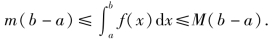
例2　估计定积dx的值的范围.

解　因为f（x）＝x2＋1在［1，3］上单调增加，所以f（1）≤f（x）≤f（3），即

根据估值定理有

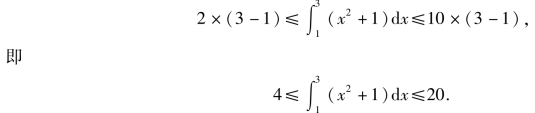
性质7（积分中值定理）　若f（x）在区间［a，b］上连续，则在［a，b］上至少存在一点ξ，使得

证明　因为f（x）在区间［a，b］上连续，则f（x）在区间［a，b］上必有最小值m和最大值M，即

由性质6，得

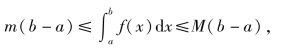
即

再由闭区间上连续函数的介值定理的推论，在［a，b］上至少存在一点ξ，使得

积分中值定理在几何上表示：在［a，b］上至少存在一点ξ，使得由曲线y＝f（x），直线x＝a，x＝b及x轴所围成的曲边梯形的面积等于以区间［a，b］为底，以f（ξ）为高的矩形的面积，如图6.4所示.

图6.4

由积分中值定理得公式f（ξ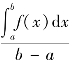）＝，表示曲线f（x）在区间［a，b］上的平均高度，称为函数f（x）在区间［a，b］上的平均值.

习题　6.2

1.比较下列各组积分值的大小.

2.估计下列积分的值.