1.曲边梯形的面积

在初等数学里，我们学习了求矩形、三角形等以直线为边的图形的面积.但在实际应用中，往往需要求以曲线为边的图形的面积，如图6.1所示.

在直角坐标系中，由闭区间［a，b］上的一条连续曲线y＝f（x）（f（x）≥0），直线x＝a，x＝b及x轴所围成的平面图形，称为曲边梯形，如图6.1所示.

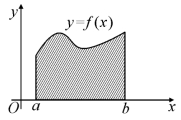
图6.1

如何计算这个曲边梯形的面积S呢？

如果f（x）恒等于常数，那么这个曲边梯形实际上是个矩形，而矩形的面积可以按公式

来计算.由于曲边梯形在底边上各点处的高f（x）在区间［a，b］上是变动的，故其面积不能直接按上述公式来计算.但是，由于曲边梯形的高f（x）在区间［a，b］上是连续变化的，在很小一段区间上它的变化很小，近似于不变.因此，如果把区间［a，b］划分为很多个小区间，在每个小区间上用其中某一点处的高来近似代替同一个小区间上各点处的小曲边梯形的高，那么，每个小曲边梯形就可近似地看成小矩形，我们把所有这些小矩形面积之和作为曲边梯形面积的近似值（图6.2）.显然，细分越细，近似程度越高.从而，将曲边梯形无限细分，所有小矩形面积之和的极限值就是曲边梯形面积的精确值.

基于上述思想，我们可以按下述步骤来计算曲边梯形的面积S：

（1）分割　在区间［a，b］内任意插入n－1个分点

将区间［a，b］分成n个小区间

第i个小区间的长度记为Δxi＝xi－xi－1（i＝1，2，…，n），过各分点xi作垂直于x轴的直线，将曲边梯形分成n个小曲边梯形，如图6.2所示.设曲边梯形的面积为S，任意小曲边梯形的面积为ΔSi（i＝1，2，…，n），则有

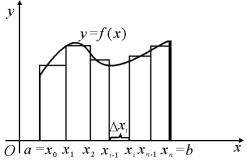
图6.2

（2）近似替代　在每个小区间［xi－1，xi］（i＝1，2，…，n）上任取一点ξi，用以小区间［xi－1，xi］的长度为底，f（ξi）为高的小矩形面积f（ξi）Δxi，近似代替第i个小曲边梯形的面积ΔSi，即

(www.daowen.com)

（3）求和　把n个小矩形的面积相加，就得到曲边梯形面积的近似值，即

（4）取极限　记λ＝max｛Δx1，Δx2，…，Δxn｝，当λ→0时，分点的个数无限增多，上面和式的极限如果存在，就定义为曲边梯形面积的精确值，即

2.变速直线运动的路程

设物体做直线运动，已知速度v＝v（t）（v（t）≥0）是时间t在时间间隔［T1，T2］上的连续函数，求这段时间内物体所经过的路程s.

若物体做匀速直线运动，即速度为常量，则有公式

这里速度是确定的.但是，当物体做变速直线运动时，其速度是变量，因此不能采用上述公式来计算路程.然而，由于速度函数v＝v（t）是连续变化的，在很短的一段时间内，速度的变化量是很微小的，可以近似地看作匀速运动，于是完全可以仿照求曲边梯形面积的方法来求变速直线运动的路程s.具体做法如下：

（1）分割　在时间间隔［T1，T2］中任意插入n－1个分点

将区间［T1，T2］分成n个小区间

第i个区间的长度记为Δti＝ti－ti－1（i＝1，2，…，n），相应地第i个小区间［ti－1，ti］上物体经过的路程记为Δsi（i＝1，2，…，n）.

（2）近似替代　在每个小区间［ti－1，ti］（i＝1，2，…，n）上任取一点ξi，取v（ξi）作为该段时间的速度，则该时间段的近似路程为

（3）求和　把n个小区间的路程Δsi的近似值相加，就得到在［T1，T2］时段上路程的近似值，即

（4）取极限　记λ＝max｛Δt1，Δt2，…，Δtn｝，当λ→0时，分点的个数无限增多，上面和式的极限如果存在，就定义为所求路程的精确值，即