1.填空题

（1）设∫xf（x）dx＝arcsinx＋C，则＝________；

（2）设f（x）的一个原函数为ln（x＋），则∫xf（x）dx＝________；

（3）________；

（4）若∫f（x）dx＝F（x）＋C，则∫e－xf（e－x）dx＝________；

（5）若∫f（x）dx＝x2e2x＋C，则f（x）＝________.

2.选择题

（1）设f（x）的一个原函数为e－2x，则f（x）＝（　）

A.e－2x

B.－2e－2x

C.－4e－2x

D.4e－2x

（2）若f（x）为连续函数，且∫f（x）dx＝F（x）＋C，则下列各式中正确的是（　）

A.∫f（xα）xα－1dx＝F（xα）＋C

B.∫f（cosx）sinxdx＝F（cosx）＋C

C.∫f（ax）axdx＝F（ax）＋C

D.∫f（lnx）(www.daowen.com)

（3）若f（x）的导数是sinx，则下列函数为f（x）的一个原函数的是（　）

A.1＋sinx

B.1－sinx

C.1＋cosx

D.1－cosx

（4）设f（x）＝e－x，则（　）

（5）若∫f（x）dx＝x2＋C，则∫xf（1－x2）dx＝（　）

3.计算下列不定积分.

4.若二阶可导函数f（x）的一个原函数为ex2，求∫x2f′′（x）dx.

5.设f′（lnx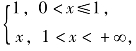）＝求f（x）和f（lnx）.

6.设某商店每周生产x单位商品时边际成本为0.3x＋8（元／单位），固定成本为100元.

（1）求总成本函数C（x）；

（2）若该商品的需求函数为x＝320－4P，求利润函数L（x）；

（3）每周生产多少单位可获得最大利润？最大利润是多少？

请使用木马课堂APP扫码完成练习