【摘要】:如果不定积分∫f(x)dx用直接积分法或凑微分法不易求得,但适当地选择变量代换x=φ(t),将原积分转换成∫f[φ(t)]φ′(t)dt的形式,此时该积分可以求出,然后回代变量t为φ-1(x),即可求出积分∫f(x)dx.我们称这种计算不定积分的方法为第二类换元积分法.定理2设x=φ(t)是单调可导函数,且φ′(t)≠0,又设f[φ(t)]φ′(t)具有原函数F(t),则其中t=φ-1(x)是x
如果不定积分∫f(x)dx用直接积分法或凑微分法不易求得,但适当地选择变量代换x=φ(t),将原积分转换成∫f[φ(t)]φ′(t)dt的形式,此时该积分可以求出,然后回代变量t为φ-1(x),即可求出积分∫f(x)dx.我们称这种计算不定积分的方法为第二类换元积分法.
定理2 设x=φ(t)是单调可导函数,且φ′(t)≠0,又设f[φ(t)]φ′(t)具有原函数F(t),则

其中t=φ-1(x)是x=φ(t)的反函数.
证明 由于F(t)是f[φ(t)]φ′(t)的原函数,所以有
![]()
由题意知F[φ-1(x)]是由F(t)和t=φ-1(x)复合而成,则根据复合函数和反函数的求导法则知,F[φ-1(x)]是f(x)的一个原函数,故有
![]()
第二类换元积分法的关键在于根据被积函数的特征,寻找一个适当的代换x=φ(t),将不定积分的计算变得简单.下面我们将介绍几类常见的变量代换类型.
1.根式代换

2.三角代换
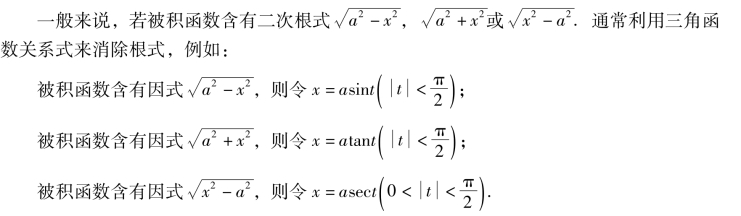
我们把上述代换称为三角代换.使用三角代换求解不定积分时,在将t回代为x时,可以根据代换式x=φ(t)的形式,构造一个以t为锐角的直角三角形,将会使变量的回代变得简单.下面举例说明.
 (https://www.daowen.com)
(https://www.daowen.com)

图5.2
3.倒代换
一般来说,如果有理分式函数中分母(多项式)的次数较高时,常采用倒代换,即令![]()

为了以后计算不定积分方便,我们将几个重要的积分公式补充到基本积分表中,以便在以后的积分计算中引用.
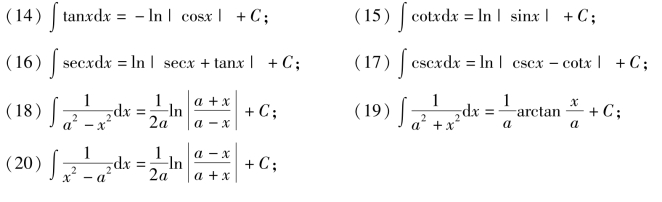

习题 5.2
1.填空题:

2.计算下列不定积分:
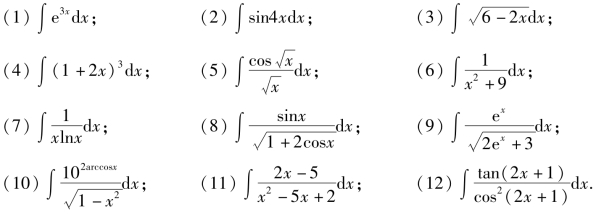
3.计算下列不定积分:
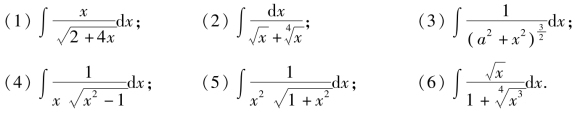
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






