1.闭区间上函数的最值

闭区间上的连续函数一定有最大值和最小值.函数最值和极值是两个不同的概念，极值只能在区间的内部取得，而最值却既可以在区间内部取得，也可以在区间端点处取得；如果函数最值点在区间的内部取得，则最值点一定是函数的极值点.

要求函数f（x）在闭区间［a，b］上的最值点，只需在函数f（x）的开区间（a，b）内的极值点及两个端点中寻找.由此可得求闭区间［a，b］上连续函数f（x）的最值的一般步骤如下：

（1）求函数f（x）在开区间（a，b）内所有的驻点以及导数f′（x）不存在的点：x1，x2，…，xn；

（2）计算函数值f（x1），f（x2），…，f（xn），f（a），f（b）；

（3）将上述函数值加以比较，最大的就是f（x）在［a，b］的最大值，最小的就是f（x）在［a，b］的最小值.

例1　求函数f（x）＝3x－x3在［－3，3］的最大值和最小值.

解　函数f（x）＝3x－x3在［－3，3］上连续，所以在该区间上存在最大值和最小值.

又因为f′（x）＝3－3x2，令f′（x）＝0，得驻点x1＝1，x2＝－1.由于

所以比较各值可得函数f（x）＝3x－x3的最大值为f（－3）＝18，最小值为f（3）＝－18.

例2　求函数f（x）＝在闭区间［0，3］上的最大值与最小值.

解　函数f（x）在闭区间［0，3］上连续，且

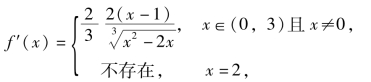
令f′（x）＝0，得驻点x＝1.(www.daowen.com)

驻点和一阶导数不存在点处的函数值分别为

在区间端点处的函数值分别为

对比上述函数值的大小，则函数f（x）在［0，3］的最大值为f（3）＝最小值f（0）＝f（2）＝0.

注1：若f（x）在一个区间内（开区间，闭区间或无穷区间）只有一个极大值点，而无极小值点，则该极大值点一定是最大值点.对于极小值点也可得出同样的结论.

注2：若函数f（x）在［a，b］上单调增加（或减少），则f（x）必在区间［a，b］的两端点上达到最大值和最小值.

2.实际问题应用举例

对于实际问题，往往根据问题的性质就可断定函数f（x）在定义区间的内部确有最大值或最小值.理论上可以证明：若实际问题断定f（x）在其定义区间内部（不是端点处）存在最大值（或最小值），且f′（x）＝0在定义区间内只有唯一一个根x0，那么，可断定，f（x）在点x0处取得相应的最大值（或最小值）.

例3　要做一个容积为V的圆柱形罐头筒，怎样设才能使所用材料最省？（如图4.11）

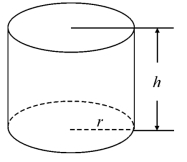
图4.11

解　使材料最省，就是要罐头筒的表面积最小，设罐头的底半径为r，高为h，如图4.11所示，则它的侧面积为2πrh，底面积为πr2，因此表面积为s＝2πr2＋2πrh.由体积公式V＝πr2h有，

于是得出结论：当所做罐头筒的高和底直径相等时，所用材料最省.