函数的图形有助于直观上了解函数的性质，所以研究函数图形的描绘很有必要.我们可以利用函数的一阶导数讨论了函数的单调性和极值，利用函数的二阶导数研究了曲线的凹凸性和拐点.此外，我们还学习了求渐近线的方法.这样我们就掌握了函数的基本性态.我们还可以利用之前学的确定函数的单调性、奇偶性、间断点以及函数与坐标轴的交点等，由此可比较准确地描绘函数的图形.

描绘函数图形的一般步骤如下：

（1）确定函数f（x）的定义域及函数具有的某些特性（如奇偶性、周期性等），并求函数的一阶导数f′（x）和二阶导数f″（x）；

（2）求出f′（x）＝0和f″（x）＝0在定义域内的所有实根以及一阶导数f′（x）和二阶导数f″（x）在定义域内不存在的点；

（3）用（2）中得到的所有点将定义域分成若干个部分区间，确定f′（x）和f″（x）在这些区间的符号，并由此确定函数的单调性、极值，函数图形凹凸性及拐点；

（4）确定曲线的渐近线（水平渐近线，铅锤渐近线，斜渐近线）；

（5）算出极值点处的函数值，拐点坐标，定出图形上相应的点；为了把图形描绘得准确有时还需补充一些点，如与坐标轴的交点等.最后结合以上得到的结果，描绘出函数y＝f（x）的图形.

例6　描绘函数f（x）＝的图形.

解　（1）函数的定义域（－∞，＋∞），因为f（－x）＝f（x），则函数是偶函数，图形关于y轴对称.

（2）确定函数的单调区间、极值、凹凸性与拐点.

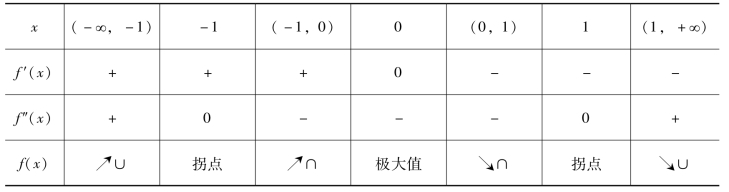
注：其中↗∪表示单调增加并且是凹的，↗∩表示单调增加并且是凸的，↘∩表示单调减少并且是凸的，↘∪表示单调减少并且是凹的.

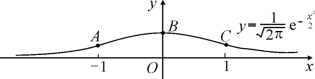
图4.9

解　（1）函数的定义域（－∞，1）∪（1，＋∞）.(www.daowen.com)

（2）确定函数的单调区间、极值、凹凸性与拐点.

注：其中↗∪表示单调增加并且是凹的，↗∩表示单调增加并且是凸的，↘∩表示单调减少并且是凸的，↘∪表示单调减少并且是凹的.

（5）曲线与x轴的交点为（－1，0），曲线没有拐点，根据上述结论描绘如图4.10所示.1.求下列函数的凹凸性及拐点.

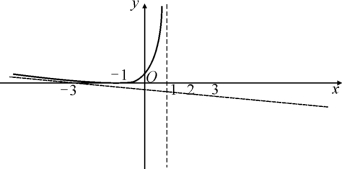
图4.10

习题　4.4

（1）y＝3x2－x3；　（2）y＝ln（1＋x2）；

（3）y＝x＋；　（4）y＝xe－x.

2.求a，b为何值时，点（1，2）为曲线y＝ax3＋bx2的拐点.

3.求下列曲线的渐近线.

4.证明曲线y＝x无拐点.

5.做出下列函数的图形.

（1）f（x）＝x3－x2－x＋1；　（2）f（x）＝x＋