如图4.6所示可以看出，曲线ACB是向下弯曲的，其上每一点的切线都位于曲线的上方，称曲线是凸的；曲线ADB是向上弯曲的，其上每一点的切线都位于曲线下方，称曲线是凹的.

从几何直观上进行分析，当曲线向上弯曲时，在曲线y＝f（x）上任取两点A，B，弦AB都在曲线弧的上方；当曲线向下弯曲时，在曲线y＝f（x）上任取两点A，B，弦AB都在曲线弧的下方；由此给出曲线凹凸性的定义.

定义1　设函数y＝f（x）在区间（a，b）上连续，在（a，b）上任取两点x1，x2，若恒有

通常，把曲线所具有的凹或凸的性质，称为曲线的凹凸性.（如图4.7）

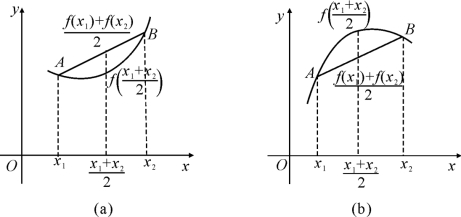
图4.7

我们如果利用定义来判别曲线的凹凸性是特别困难的.由图4.6，当凹曲线上的切点从A→D→B移动时，其对应的切线斜率f′（x）是单调增加的；当凸曲线上的切点从A→C→B移动时，其对应的切线斜率f′（x）是单调减少的，根据单调性与导数的关系，当二阶导数f″（x）存在时，可用二阶导数的符号来判别曲线的凹凸性.

定理1　设函数y＝f（x）在［a，b］上连续，在（a，b）内具有二阶导数，则：

（1）若x∈（a，b）时，f″（x）＞0，则曲线y＝f（x）在（a，b）上是凹的；

（2）若x∈（a，b）时，f″（x）＜0，则曲线y＝f（x）在（a，b）上是凸的.

证　∀x1，x2∈［a，b］，且x1＜x2，记x0＝并记x2－x0＝x0－x1＝h，对函数y＝f（x）在区间［x1，x0］，［x0，x2］上应用拉格朗日中值公式，得

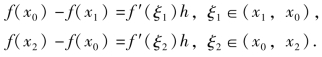
上述两式相减，得(www.daowen.com)

对f′（x）在区间［ξ1，ξ2］上再应用拉格朗日中值公式，得

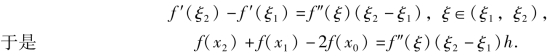
（1）若x∈（a，b）时，f″（x）＞0，则f″（ξ）＞0，由于h＞0，ξ2－ξ1＞0，所以有

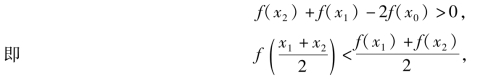
因此，曲线y＝f（x）在（a，b）上是凹的.

（2）若x∈（a，b）时，f″（x）＜0，则f″（ξ）＜0，由于h＞0，ξ2－ξ1＞0，所以有

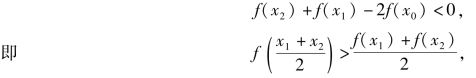
因此，曲线y＝f（x）在（a，b）上是凸的.

例1　求曲线y＝x3凹凸区间.

解　函数y＝x3的定义域为（－∞，＋∞），

当x∈（－∞，0）时，y″＜0，曲线y＝x3是凸的；

当x∈（0，＋∞）时，y″（x）＞0，曲线y＝x3是凹的.