函数极值是一个局部性概念，其定义如下：

定义1　设函数f（x）在点x0的某个邻域内U（x0）有定义，对任意x∈U。（x0），

（1）若f（x）＜f（x0），则称x0是函数f（x）的极大值点，称f（x0）为函数f（x）的极大值；

（2）若f（x）＞f（x0），则称x0是函数f（x）的极小值点，称f（x0）为函数f（x）的极小值.

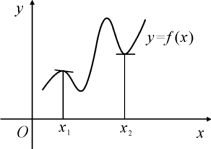
图4.5

函数的极大值与极小值统称为极值.极大值点和极小值点称为极值点.（如图4.5）

注（1）极值是局部的一个概念，它仅与极值点左右邻域的函数值的大小有关.

（2）极值往往可能有很多个，且某一点取得的极大值可能会比另一点取得的极小值还小.

（3）由极值点的定义知，函数的极值点只可能在区间的内部取得.

定理2（极值的必要条件）　若函数f（x）在x处可导，且在x0处取得极值，则f′（x0）＝0.

证　假设x0是极大值点，由极大值的定义知，存在x0的某邻域U（x0），对任意时，有f（x）＜f（x0），即f（x）－f（x0）＜0，

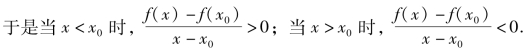
又因为f（x）在x0处可导，所以f′－（x0）＝f′＋（x0）＝f′（x0），根据导数的定义与极限的保号性有

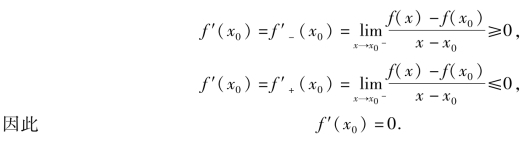
由定理2可知可导函数的极值点必为驻点，反之，驻点不一定是极值点，例如：函数y＝x3的驻点为x＝0，但x＝0不是函数的极值点，函数y＝x3在（－∞，＋∞）内单调增加.，在x＝0处导数不存在，但由图象可知x＝0是它的极值点.所以f′（x0）不存在时，x0也可能为极值点.综上所述，极值点可能是驻点或f′（x）不存在的点.

定理3（极值存在的第一充分条件）　设函数f（x）在x0的某邻域U（x0）内连续，在x0的去心邻域U。（x0）内可导，x0为函数f（x）的驻点或导数不存在的点，

（1）若对任意x∈（x0－δ，x0），f′（x）＞0；若对任意x∈（x0，x0＋δ），f′（x）＜0，则x0

连续而不可导的点也有可能是极值点，例如y＝是极大值点，f（x0）为极大值；

（2）若对任意x∈（x0－δ，x0），f′（x）＜0；若对任意x∈（x0，x0＋δ），f′（x）＞0，则x0是极小值点，f（x0）为极小值；

（3）若在x0的去心邻域U。（x0）内f′（x）不变号，那么x0不是极值点，函数f（x）在x0处无极值.

证　（1）由假设知，f（x）在x0的左侧邻域单调增加；在x0的右侧邻域单调减少，即当x＜x0时，f（x）＜f（x0）；当x＞x0时，f（x）＜f（x0），因此x0是f（x）的极大值点，f（x0）是f（x）的极大值.

类似可以证明（2）.

（2）由假设，当x在x0的某个邻域（x≠x0）内取值时，f′（x）＞0（或＜0），所以，在这个邻域内是单调增加（减少）的，因此x0不是极值点.证毕.

求函数的极值点时，可以先求出全部可能成为极值点的点（即驻点和导数不存在的点），从而按照极值存在的第一充分条件判断函数的极值，具体步骤如下：

（1）在函数的定义域内，求出全部可能成为极值点的点（即驻点和导数不存在的点）；

（2）考查每个驻点和导数不存在的点的两侧f′（x）是否变号，从而确定这些点是否为极值点；

（3）求出各极值点处的函数值.

例5　求出函数f（x）＝x3－3x2－9x＋5的极值.

解　函数f（x）＝x3－3x2－9x＋5的定义域为（－∞，＋∞），且

令f′（x）＝0，得驻点x1＝－1，x2＝3，

在（－∞，－1）内，f′（x）＞0；在（－1，3）内，f′（x）＜0；在（3，＋∞）内，f′（x）＞0，由定理3知，f（－1）为函数f（x）的极大值，f（3）为函数f（x）的极小值.即f（x）在x＝－1取得极大值：f（－1）＝10；f（x）在x＝3取得极小值：f（3）＝－22.(www.daowen.com)

定理4（极值的第二充分条件）　设f（x）在点x0处具有二阶导数，且f′（x0）＝0，f″（x0）≠0，

（1）如果f″（x0）＜0，那么函数在x0处取极大值f（x0）；

（2）如果f″（x0）＞0，那么函数在x0处取极小值f（x0）.

证（1）由于f″（x0）＜0，f′（x0）＝0，所以由导数的定义，得

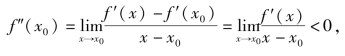
所以当x∈U。（x0，δ）时，根据极限的保号性有

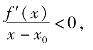
从而知道，当x∈（x0－δ，x0）时，f′（x）＞0；当x∈（x0，x0＋δ）时，f′（x）＜0，由定理3知f（x0）为f（x）的极大值.类似地可证明（2），证毕.

例7　求函数f（x）＝cos2x＋2sinx（0＜x＜π）的极值.

解　f′（x）＝－2sin2x＋2cosx＝2cosx（1－2sinx），

f″（x）＝－4cos2x－2sinx，

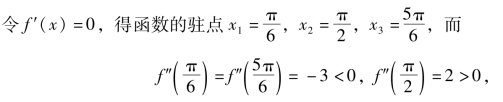
所以由定理4得是函数的极大值，是函数的极小值.

例8　求函数f（x）＝4＋8x3－3x4的极值.

解　函数f（x）的定义域（－∞，＋∞），

令f′（x）＝0，得驻点x1＝0，x2＝2，则f″（2）＝－48＜0，根据定理4知f（2）＝20时极大值.

但，因为f″（0）＝0，则在驻点x1＝0处极值存在的第二充分条件失效，这时选用第一充分条件判定，当x∈（－∞，0）时，f′（x）＞0；当x∈（0，2）时，f′（x）＞0，由定理3知x＝0时函数不取极值.

注　f′（x0），f″（x0）不存在或f″（x0）＝0时，第二判别法失效，此时应用第一判别法或定义来判定.

习题　4.3

1.求下列函数的单调性.

2.利用函数单调性证明下列不等式.

（3）当x＞a＞e时，ax＞xa.

3.求下列函数的极值.

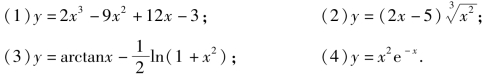
4.利用极值存在的第二充分条件求下列函数极值.

（1）y＝2x3－6x2＋1；　（2）y＝x3（3x－5）2.

5.证明函数y＝x＋在其定义域内单调增加的.

6.设f（x）＝alnx＋bx2＋x，在x1＝1，x2＝2处都取得极值；试确定a和b的值，并指出f（x）在x1和x2处取得极大值还是极小值.