定理3（柯西中值定理）　如果函数f（x），F（x）满足下列条件：

（1）在闭区间［a，b］上连续；

（2）在开区间（a，b）内可导，且F′（ξ）≠0；则至少存在一点ξ∈（a，b），使得

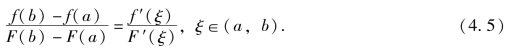
证　首先明确F（b）≠F（a），假设F（b）＝F（a），有罗尔定理知，至少存在一点ξ∈（a，b），使得F′（ξ）＝0，与假设条件（2）矛盾，故F（b）≠F（a）.

作辅助函数

由假设条件知L（x）在闭区间［a，b］上连续，在开区间（a，b）内可导，且

于是L（x）在［a，b］上满足罗尔中值定理，故至少存在一点ξ∈（a，b），使得L′（ξ）＝0，

即

因此

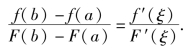
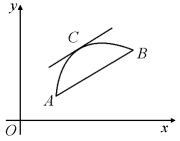
图4.3

几何解释如下：将定理中的x看成参数，则可将X＝F（x），Y＝f（x），x∈（a，b）看作一条曲线的参量方程表达式，则由柯西中值定理的几何意义就表示：在连续且除端点外处处有不垂直于x轴的曲线至少存在一点C，使该点处的切线平行于两端点的连线（如图4.3）.(www.daowen.com)

特别地，当F（x）＝x，则F（b）－F（a）＝b－a，F′（ξ）＝1，（4.5）式就成了（4.1）式，可见拉格朗日中值定理是柯西中值定理的特殊情形.

例6　设函数f（x）在闭区间［a，b］（a≥0）上连续，在开区间（a，b）内可导，证明：在开区间（a，b）内至少存在一点ξ，使得

证　作辅助函数g（x）＝x2，显然g（x）在闭区间［a，b］上连续，在开区间（a，b）内可导，且g′（x）＝2x≠0，所以，f（x），g（x）在闭区间［a，b］上满足柯西中值定理的条件，在开区间（a，b）内至少存在在一点ξ，

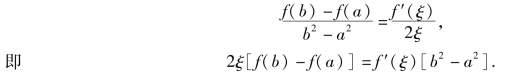
习题　4.1

1.验证下列函数是否满足罗尔中值定理的条件？如果满足，求出定理中的ξ值.

（1）f（x）＝x3－x，x∈［－1，1］；　（2）f（x）＝

2.验证下列函数是否满足拉格朗日中值定理的条件？如果满足，求出定理中的ξ值.

（1）f（x）＝arctanx，x∈［0，1］；　（2）f（x）＝x3＋2x，x∈［0，1］.

3.证明方程5x4－4x＋1＝0在0和1之间至少有一实根.

4.设函数f（x）在闭区间［0，1］上连续，在开区间（0，1）内可导，且f（1）＝0，试证在（0，1）内至少存在一点ξ，使得f′（ξ）＝

5.证明下列各式.

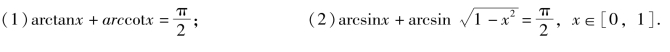
6.设f（x），g（x）在闭区间［a，b］上连续，在开区间（a，b）内可导，且f（a）＝f（b）＝0，g（x）≠0，试证：至少存在一点ξ∈（a，b），使得