定理2(拉格朗日中值定理) 如果函数f(x)满足下列条件:
(1)f(x)在闭区间[a,b]上连续;
(2)f(x)在开区间(a,b)内可导,
![]()
证 作辅助函数

由假设条件知F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且
![]()
所以F(x)在[a,b]上满足罗尔中值定理,故至少存在一点ξ∈(a,b),使得f′(ξ)=0,即
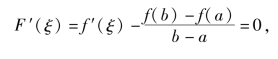
因此
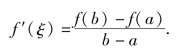
拉格朗日中值定理的几何意义:在满足拉格朗日中值定理中(1)、(2)条件的曲线段![]() 上,至少有一点处的切线平行于弦AB(如图4.2).
上,至少有一点处的切线平行于弦AB(如图4.2).
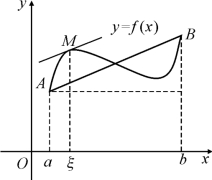
图4.2
拉格朗日中值定理是微分学的一个基本定理,在理论上和应用上都有很重要的价值,它建立了函数在一个区间上的改变量和函数在这个区间内某点处的导数之间的联系,从而使我们有可能用导数去研究函数在区间上的性态.
由定理的结论我们可以看到,拉格朗日中值定理是罗尔定理的推广,它是由函数的局部性质来研究函数的整体性质的桥梁,其应用十分广泛,读者将会在今后应用中看到.式(4.1)也称为拉格朗日中值公式,还可以写成
![]()
由于ξ是(a,b)中的一个点,故可表示为ξ=a+θ(b-a),(0<θ<1)的形式,所以拉格朗日中值公式还可写成
![]()
若我们把a与b分别换成x与x+Δx,则b-a=Δx,于是,拉格朗日中值公式就写成
![]()
我们也称公式(4.4)为有限增量公式.
要注意的是,在公式(4.2)中,无论a<b或a>b公式总是成立的,其中ξ是介于a与b之间的某个数.同样公式(4.4)中无论Δx<0或Δx>0都成立.(www.daowen.com)
由拉格朗日中值定理可以得出积分学中有用的推论.
推论1 如果函数f(x)在区间(a,b)内满足f′(x)≡0,则在(a,b)内f(x)=C(C为常数).
证 取一定点x0∈(a,b),只需证明f(x)=f(x0)即可.因为f(x)在(a,b)内可导,所以f(x)在以x0和x为端点的闭区间上连续,开区间内可导,从而由拉格朗日中值定理知,存在ξ在x0与x之间,使
![]()
即f(x)=f(x0).
再由x0的固定性和x的任意性知,∀x∈(a,b),均有f(x)=f(x0),则在(a,b)内f(x)≡C(常数).
推论2 如果对(a,b)内任意x,均有f′(x)=g′(x),则在(a,b)内f(x)与g(x)之间只差一个常数,即f(x)=g(x)+C.
证 令F(x)=f(x)-g(x),则F′(x)=0,由推论1知,F(x)在(a,b)内为一个常数C,即f(x)=g(x)+C,x∈(a,b),证毕.
例3 验证f(x)=x2在[0,1]上拉格朗日中值定理的正确性.
解 显然f(x)=x2在[0,1]上连续,在(0,1)内可导,故至少存在一点ξ∈(0,1),使f(1)-f(0)=f′(ξ)(1-0),
下面求出具体的ξ,由f(1)-f(0)=f′(ξ)(1-0),
![]()
即确实存在ξ=![]() 使f(1)-f(0)=f′(ξ)(1-0)成立.
使f(1)-f(0)=f′(ξ)(1-0)成立.
例4 证明
![]()
证 令f(x)=arcsinx+arccosx,则有
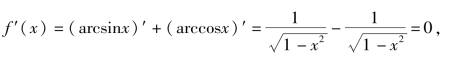
由推论1可知,在x∈(-1,1)内恒有

例5 证明不等式
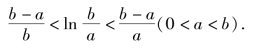
证 设f(x)=lnx,则函数在闭区间[a,b]上连续,在开区间(a,b)内可导,且![]() 则函数f(x)=lnx满足拉格朗日中值定理,至少存在一点ξ∈(a,b),使得
则函数f(x)=lnx满足拉格朗日中值定理,至少存在一点ξ∈(a,b),使得
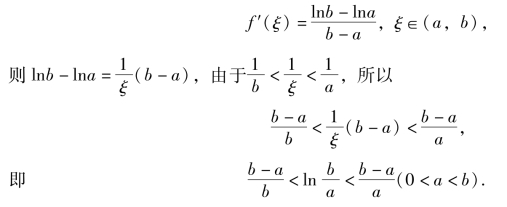
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





