定理1（罗尔中值定理）　如果函数y＝f（x）满足下列条件：

（1）f（x）在闭区间［a，b］上连续；

（2）f（x）在开区间（a，b）内可导；

（3）f（a）＝f（b）；

则至少存在一点ξ∈（a，b），使f′（ξ）＝0.

证　因为f（x）在［a，b］上连续，根据闭区间上连续函数的性质，f（x）在闭区间［a，b］上必取得最大值M和最小值m.

（1）如果M＝m，f（x）在闭区间［a，b］上恒等于常数M，因此，对一切x∈（a，b），都有f′（x）＝0.

（2）若M＞m，由于f（a）＝f（b），所以M和m中至少有一个不等于f（a）.不妨设M≠f（a），证明过程完全类似，则f（x）应在（a，b）内的某一点ξ处达到最大值，即f（ξ）＝M，下面证f′（ξ）＝0.

因为ξ∈（a，b），由定理假设（2）知f′（ξ）存在，所以有

又因为f（x）在ξ处达到最大值，所以不论Δx是正还是负的只要ξ＋Δx∈（a，b），总有

当Δx＞0时，有

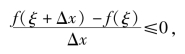
根据极限的保号性及f′（ξ）存在知

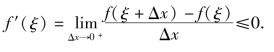
当Δx＜0时，有(www.daowen.com)

于是

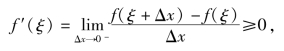
由上述知

罗尔中值定理的几何意义是：在两个高度相同的点A，B之间的一段连续曲线上，如果除端点外处有不垂直于x轴的切线，则在弧AB上曲线至少有一条水平切线，如图4.1所示.

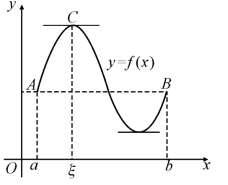
图4.1

例1　验证罗尔定理对函数f（x）＝x2－2x＋3在［－1，3］上的正确性.

解　函数f（x）＝x2－2x＋3在闭区间［－1，3］上连续，在开区间（－1，3）上可导，且f（－1）＝f（3）＝6，由f′（x）＝2x－2可知，f′（1）＝0，因此存在ξ＝1∈（－1，3），使得f′（1）＝0.

例2　不求函数f（x）＝（x－1）（x－2）（x－3）的导数，证明方程f′（x）＝0有几个实根，并指出这些根所在的区间.

解　因为f（1）＝f（2）＝f（3）＝0，所以f（x）在闭区间［1，2］、［2，3］上均满足罗尔定理的三个条件，根据罗尔定理可得，在开区间（1，2）内至少存在一点ξ1，在开区间（2，3）内至少存在一点ξ2，使得

所以方程f′（x）＝0至少有两个实根.

又因为f′（x）＝0是一个一元二次方程，至多有两个实根，从而方程f′（x）＝0有且只有两个实根，分别在开区间（1，2）和（2，3）内.