1.填空题

（1）f（x）在x0可导是在x0连续的______条件，f（x）在点x0连续是f（x）在点x0可导的________条件；

（2）f（x）在x0的左导数右导数都存在且相等是f（x）在点x0可导的________条件；

（3）f（x）在点x0可导是f（x）在点xo可微的________条件；

（4）已知f′（2）＝2，则________；

（5）d______＝sin2xdx；

（6）设函数f（x）＝x（x－1）（x－2）…（x－99），则f′（0）＝________；

（7）设方程exy＋y2＝cosx确定y是x的函数，则________；

（8）设y＝f（lnx）ef（x），其中f可微，则dy＝________.

2.选择题

（1）已知下列各极限都存在，且可导，则下列选项不正确的题（　）

（2）若f（x）为（－∞，＋∞）内的奇函数，在（－∞，0）内f′（x）＞0，且f″（x）＜0，则在（0，＋∞）内有（　）

A.f′（x）＞0，f″（x）＜0

B.f′（x）＜0，f″（x）＜0

C.f′（x）＞0，f″（x）＞0

D.f′（x）＜0，f″（x）＞0

（3）若函数f（x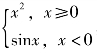）＝，则f（x）在点x＝0处（　）

A.导数为1

B.导数不存在

C.导数为2

D.导数为0

（4）设函数f（x）在x＝a处可导，则函数在点x＝a处不可导的充要条件是（　）

A.f（a）＝0，且f′（a）＝0(www.daowen.com)

B.f（a）＝0，且f′（a）≠0

C.f（a）＞0，且f′（a）＞0

D.f（a）＜0，且f′（a）＜0

3.讨论函数

在x＝0处的连续性和可导性.

4.求下列函数的导数.

5.求下列函数的微分.

（1）y＝e3x；　（2）y＝esinx2；

（3）y＝arctan2x；　（4）y＝

6.求下列隐函数的导数.

7.求下列函数的二阶导数.

（1）y＝（1＋x2）arctanx；

（2）y＝xsin3x；

（3）y＝（x3＋1）2；

（4）y＝ln（1＋x2）.

8.设某糕点加工厂生产A类糕点的总成本函数和总收入函数分别为C（Q）＝100＋2Q＋0.02Q2和R（Q）＝7Q＋0.01Q2，求边际利润函数和当日产量分别是200kg、250kg和300kg时的边际利润，并说明其经济意义.

9.设某商品的价格P与销售量Q的关系为P（Q）＝104－0.4Q.

（1）求边际收益；

（2）求销售量为Q＝50个单位时的边际收益，并给出经济解释；

（3）求销售量为Q＝100个单位时总收益对Q的弹性，并给出经济解释.

请使用木马课堂APP扫码完成练习