在物理中，变速直线运动的速度v（t）是位置函数s（t）对时间t的导数，即

而加速度a（t）又是速度v（t）对时间t的变换率，即速度v（t）对时间t的导数，所以

上述导数的导或［s′（t）］′称为s（t）对时间t的二阶导数，记作

如果函数y＝f（x）的导数y′＝f′（x）仍是x的可导函数，就称y′＝f′（x）的导数为函数y＝f（x）的二阶导数，记作y″，f″（x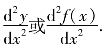

类似地，二阶导数的导数叫作三阶导数，三阶导数的导数叫作四阶导数，一般地，n－1阶的导数叫作n阶导数，分别记作

通常我们称二阶及二阶以上的导数为高阶导数.显然，求高阶导数并不需要更新的方法，只要逐阶求导，一直求到所要求的阶数即可，所以仍可用前面学过的求导方法来计算高阶导数.

例1　已知函数y＝arctanx，求y″.

例2　设f（x）＝xlnx，求f″（1）.

例3　求函数y＝－4x3＋5x2－6x＋的各阶导数.

解　y′＝－12x2＋10x－6，y″＝－24x＋10，y‴＝－12，…，则

下面介绍几个初等函数的n阶导数.

例4　求幂函数y＝xμ，（μ为任意常数）的n阶导数.

例5　求指数函数y＝ax（a＞0，a≠1）的n阶导数.

解　y′＝axlna，y″＝ax（lna）2，y‴＝ax（lna）3，

例6　求正弦函数y＝sinx的n阶导数.

例7　求函数y＝ln（1＋x）的n阶导数.(www.daowen.com)

高阶导数的运算法则：

设函数u（x），v（x）均有n阶导数，则

上式也称为莱布尼茨公式.

习题　3.3

1.求下列函数的二阶导数.

（1）y＝ln（1＋x2）；　（2）y＝

（3）y＝exsinx；　（4）y＝ln（x＋

2.设函数f（x）＝，求f″（0），f″（1）和f″（－1）.

3.求f（x）＝ln（1－x）的n阶导数.

4.验证函数y＝exsinx满足关系式y″－2y′＋2y＝0.

5.设函数的二阶导数存在，求下列复合函数的二阶导数y″.

（1）y＝f（x3）；　（2）y＝lnf（x）（f（x）＞0）.

6.求下列函数所指定的阶的导数.

（1）y＝x3ex，求y（10）；　（2）y＝excosx，求y（4）.