1.做变速直线运动物体的瞬时速度

设有一质点沿直线运动，其位移时间的函数关系s＝s（t），求物体在任意时刻t0的瞬时速度v（t0）.

由物理学知，物体做匀速直线运动时，可来求质点的运动速度，而物体做非匀速直线运动时，就不能简单地用来描述物体运动的速度了，此时，设在t0时刻物体的位置坐标为s（t0），当时间由t0变到t0＋Δt时，物体在这一时间段内所经过的路程为

于是这一段时间内物体运动的平均速度为

易见Δt充分小，Δt时间内的平均速度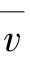的值就无限接近t0时刻的速度；因此，当Δt→0时，平均速度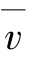的极限就为物体在t0时刻的瞬时速度，即

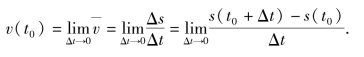
2.平面曲线的切线

在中学数学的平面几何中，圆锥曲线的切线定义为与曲线只有一个交点的直线，这种定义很有局限性，仅适用于少数几种曲线，例如圆锥曲线等；而对于一般的平面曲线而言，我们给出曲线切线的定义.(www.daowen.com)

定义1　设点M（x0，y0）是曲线L的一定点，在曲线L上任取一点M1，作割线M1M，当点M1沿曲线L趋向于点M时，如果割线M1M的极限位置MT存在，则称直线MT为曲线L在点M（x0，y0）处的切线.（如图3.1）

图3.1

那么曲线的切线斜率如何计算呢？

设曲线L的方程为y＝f（x），M（x0，y0）为曲线L上的点，在点M（x0，y0）处的附近取曲线L上任意一点M1（x0＋Δx，y0＋Δy），若割线M0M与x轴夹角为φ，那么割线M1M的斜率为

当点M1沿曲线L趋向于点M时，即Δx→0时，割线M1M的极限位置存在，为切线MT，从而切线MT的斜率就应该是割线M1M斜率的极限，如图3.1所示，若其倾角α，则有

上述两个引例虽然反映的具体问题不同，但究其本质，它们讨论的都是当自变量的增量的趋于零时，函数的增量与自变量的增量比值的极限（因变量关于自变量的变化率）问题.抛开这些变量的具体意义，抓住它们在数量关系上的实质，就可引出导数的概念.