1.函数的增量

如图2.6所示，设自变量x由初值x0变到终值x，则终值x与初值x0的差x－x0称为自变量x在x0点的增量，记为Δx，即Δx＝x－x0（或x＝x0＋Δx）.Δx可正、可负、也可为零.

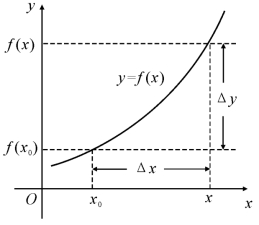
图2.6

由于x→x0（或Δx→0），于是相应地函数值的差f（x）－f（x0），称为函数f（x）在x0点的增量，记为Δy，即Δy＝f（x）－f（x0）＝y－y0，亦即f（x）＝f（x0）＋Δy（或y＝y0＋Δy）.

例1　设y＝f（x）＝3x2－1，求适合下列条件的自变量的增量Δx和相应的函数的增量Δy：（1）当x由1变为1.5；（2）当x由1变到1＋Δx.

解　（1）Δx＝1.5－1＝0.5，Δy＝f（1.5）－f（1）＝5.75－2＝3.75；

（2）自变量的增量为（1＋Δx）－1＝Δx，函数的增量Δy＝f（1＋Δx）－f（1）＝6Δx＋3（Δx）2.

2.函数的连续性

引例　某一天中水温T是随着时间t的变化而连续变化的.当t的变化Δt很微小时，水温T的变化ΔT也很微小，即当Δt→0时，ΔT→0.

函数在点x0连续，反映到图象上即函数在x0的左右是连绵不断的，也就是在x0处，当自变量的增量Δx很小时，相应的函数值的增量Δy也很小（如图2.6）.

定义1　设函数y＝f（x）在点x0及其附近有定义，＝0，则称函数f（x）在点x0连续，x0称为函数y＝f（x）的连续点.

由于Δx＝x－x0，Δy＝f（x）－f（x0），当Δx→0时，x→x0，所以y＝f（x）在点x0处连续也可写＝0，即

我们可以得到连续的另一等价定义是：

定义2　设函数y＝f（x）在点x0及其附近有定义，如果函数f（x）当x→x0时的极限存在，且等于它在点x0处的函数值f（x0），即，那么就称函数y＝f（x）在点x0连续.(www.daowen.com)

由定义2可知函数f（x）在x0处连续成立，则必须同时满足以下三个条件：

（1）函数f（x）在x0处有定义；

（2）极存在；

（3）极限值等于函数值，即

由函数的左极限和右极限的定义，我们还可引出函数的左连续和右连续的概念：如果函数y＝f（x）在x0处及其左邻域内有定义，且＝f（x0），则称函数y＝f（x）在x0处左连续.如果函数y＝f（x）在x0处及其右邻域内有定义，且＝f（x0），则称函数y＝f（x）在x0处右连续.

因此，函数y＝f（x）在x0处连续的充分必要条件是函数y＝f（x）在x0处既左连续且右连续.

例2　判断函数

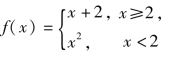
在x＝2处是否连续？

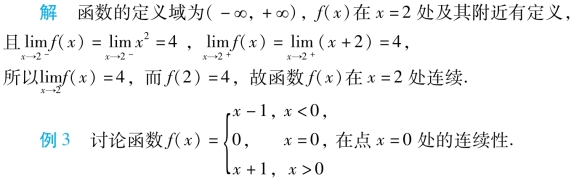
解　函数定义域为（－∞，＋∞），

即函数在x＝1处的极限值不等于函数值，故函数f（x）在x＝1处不连续.

若函数f（x）在开区间（a，b）内任何一点处都连续，则称函数f（x）在开区间（a，b）内连续；若函数f（x）在开区间（a，b）内连续，且在左端点a处右连续，在右端点b处左连续，则称函数f（x）在闭区间［a，b］上连续.

一般地，如果函数f（x）在某个区间上连续，则函数f（x）的图象是一条连续不断的曲线，因此，基本初等函数以及常数函数在其定义区间内都是连续的.