引例　我国春秋战国时期的哲学家庄周所著《庄子》记载着“一尺之棰，日取其半，万世不竭.”意思是说：一尺长的木棒，第一天取去一半，永远都取不完.如果把每天截后剩余部分按第一天、第二天、…顺序排列出来，第一天取去一半，还剩尺，第二天再在这尺中取去一半，还剩尺，…，得到如下一列数：

显然，当n无限增大时，对应的截后所剩越来越少，无限地接近于0，但是不管n多么大，它却永远不会等于零.

通过上述例子，它可以体现出一个“数列极限”的思想，因此我们可以给出数列极限的直观解释.对于一个数列{x}n，当项数n逐渐增大时，相应的xn无限接近于一个确定的常数a，常数a就是这个数列的极限.但在这里，“无限接近”是一个模糊的概念，到底如何来用准确的数学概念来表示这个“无限接近”呢？我们是不是可以通过两者之差的绝对值来衡量.例如数列当n无限增大时，无限接近于0，两个数的接近程度可以用它们之差的绝对值来衡量.因此说当n很大时，与0很接近，就是与0的距很小.

上面的式子我们可以看出当n增大时，的值无限接近于0，就是说与0的距离就可以任意小，只要n充分大，即n大于某个正整数N.因此，“无限接近”就能用距离的任意小来反映，而对于任意给定的正数ε，无论它多么小，只要N足够大，对于n＞N，都能够保也就是说，只要n＞，于是取N＝，则对大于N的所有n，上式总成立.

基于这种思想，我们对极限概念给出严格的定义.

定义2（数列极限的ε－N定义）　设数列{xn}，如果存在一个常数a，对于任意给定的ε＞0，总存在正整数N，使得当n＞N时，不等式

恒成立，则称常数a为数列{xn}当n趋于无穷大时的极限，或称数列{xn}收敛于a，记作

如果不存在常数a，则称数列{xn}没有极限，或者称数列{xn}是发散的.(www.daowen.com)

下面用极限的定义来验证数列的极限.

证明：对于任意给定的ε＞0，要使不等式

证明：对于任意给定的ε＞0，要使不等式

注：（1）在数列极限定义中，ε可以任意给定是很重要的，只要让正数ε任意小，不等式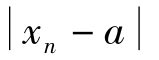＜ε才能充分表达出xn与a无限接近的意思.

（2）正整数N与ε有关，随着ε的给定而可选定，如上例中也可取N≥.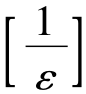

（3）数列极限定义只能验证某一个数是否为数列的极限，但不能用于求数列的极限.