1.奇偶性

定义3　给定函数y＝f（x）（x∈D），D为对称于原点的数集，如果对任意x∈D，有

恒成立，就称f（x）为偶函数.如果对任意x∈D，有

恒成立，就称f（x）为奇函数.

对于偶函数，由于f（－x）＝f（x），所以，偶函数的图形关于y轴对称；同理，奇函数的图形关于原点对称.如图1.6所示.

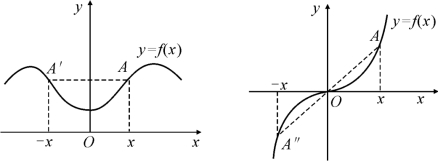
图1.6

2.单调性

定义4　设函数f（x）在区间I上有定义，若对任意两数x1，x2∈I，当x1＜x2时总有：

则称f（x）是I上的增函数，特别地，当f（x1）＜f（x2）时，就称f（x）在I上的严格增函数；

则称f（x）是I上的减函数，特别地，当f（x1）＞f（x2）时，就称f（x）在I上的严格减函数.

增函数和减函数统称为单调函数，严格增函数和严格减函数统称为严格单调函数.对有些非单调函数y＝f（x），可以将区间I划分为若干个不重叠的区间，且函数f（x）在这些区间上是单调的，则称这些区间为函数的单调区间.

例如，y＝x2在区间（－∞，＋∞）上不是单调的，但在区间［0，＋∞）上是单调增加的，在区间（－∞，0）上是单调减少的，则（－∞，0），［0，＋∞）为函数y＝x2的单调区间.

从图象上来看，函数的递增是当自变量自左向右变化时，函数的图象上升；递减就是当自变量自左向右变化时，函数的图象下降.

3.周期性

定义5　设函数f（x）的定义域为R，若存在l≠0，对于任意的x∈D，有x±l∈R，使得f（x±l）＝f（x）恒成立，就称f（x）为周期函数.(www.daowen.com)

满足上述条件的l中最小的正数称为函数的最小正周期，简称为周期.

例如，y＝sinx是周期为2π的周期函数；函数tanx是周期为π的周期函数.周期函数不一定有最小正周期，例如，常数函数是周期函数，但没有最小正周期.

4.有界性

定义6　设函数y＝f（x）在区间（a，b）内有定义，若存在一个正数M，对任意的x∈（a，b），恒有≤M，则称函数f（x）在区间（a，b）上有界，否则称为无界.

例如，y＝sinx在（－∞，＋∞）上有界，因为对任何实数x，恒有≤1；函数y＝在（0，1）内是无界的，但在［1，＋∞）上是有界的.由此可见，如果说某个函数是有界函数或无界函数必须指明所考虑的区间.

习题　1.2

1．f（x）＝x3－3x＋2，求f（0），f（1），f（2），f（－x），f（x＋1）.

2.求下列函数的定义域：

3.判断下列每对函数是否相等？为什么？

4.判断下列函数在指定区间上的单调性：

5.判断下列函数的奇偶性：

6.判断下列函数的周期性，如果是周期函数，指出其周期.

(1 )y＝sin(x－3)；(2 )y＝1＋cosπx.

7.求下列函数的反函数：

8.证明：f（x）＝xsin x在（0＋∞）上是无界函数．