在研究实际问题的过程中，常常发现有几个变量同时变化，它们并不是孤立的，它们不仅是相互联系的，而且还是遵循一定变化规律的，下面先举例说明两个变量的情形.

例1　正方形的面积S与其边长x之间的关系为S＝x2，这里面S和x都是变量，当边长x变化时，其面积S也随之做相应的变化.

例2　一个物体在高空做自由落体运动，从开始下落时算起经过的时间设为t（s），落地前在这段时间中落体的路程设为s（m）.如果只考虑重力对物体的作用，空气阻力忽略不计，由物理学知识可知s与t之间有如下的关系

其中g为重力加速度（通常取g＝9.8m／s2）.

以上两个例子所描述的问题虽各不相同，但却有共同的特征：它们都表达了两个变量之间的相互依赖关系.当一个变量在它的变化范围中任取一定值时，另一个变量按一定法则就有一个确定的值与之对应.把这种确定的依赖关系抽象出来，就是函数的概念.

1.函数的定义

定义1　设x和y为两个变量，D为一个非空实数集，若对于数集D中的每一个x，按照一定的法则f，变量y总有唯一确定的数值与之对应，就称y为x的函数，记为y＝f（x）.数集D称为该函数的定义域，x叫作自变量，y叫作因变量.

当x取数值x0∈D时，依法则f的对应值y0称为函数y＝f（x）在x＝x0时的函数值，记作f（x0）.所有函数值组成的集合M＝＝f（x），x∈D｝称为函数y＝f（x）的值域.

值得注意的是记号f和f（x）的含义是有区别的，f表示自变量x和因变量y之间的对应法则，而f（x）表示与自变量x对应的函数值.

如果x0∈D，则称函数f在点x0处有定义或有意义；如果x0∉D，则称函数f在点x0处无定义或无意义.

如果y是x的函数，有时也可记为y＝F（x），y＝g（x），y＝φ（x）或y＝ψ（x）等.当讨论到几个不同的函数时，为了区别起见，需要用不同的记号来表示它们.

由于函数的定义域和对应法则被确定后，其值域就随之而定，所以定义域和对应法则就成了函数的两个要素.如果两个函数的定义域和对应法则都相同，则称这两个函数相同，否则不同.例如函数y＝x2（x∈R）与y＝t2（t∈R），它们的定义域、值域及对应法则均一致，只是表示变量的字母不同，所以它们是两个相同的函数；可是对于函数y＝与由于它们的定义域不同，所以它们是两个不同的函数；对于函数y＝x与y＝由于它们有相同的定义域，但值域不同，所以它们不是相同的函数.

在研究函数时必须注意它的定义域.在实际问题中，函数的定义域是根据问题的实际意义来确定的.如例1中定义域为D＝（0，＋∞），例2中定义域为D＝［0，T］.

而在数学中，有时不考虑函数的实际意义，而抽象地研究用算式表达的函数，这时约定函数的定义域是为了使得这个式子的运算有意义的所有实数值，这种定义域又称为函数的自然定义域.

通常情况下，求函数定义域时应遵循以下一些原则：

（1）偶次根式的函数，其根号下的值非负；

（2）分式函数，分母的值不能为零；

（3）有限个函数的四则运算得到的新的函数，其定义域为这有限个函数定义域的交集；

（4）对数函数的真数值必须是正数；

（5）对有实际背景的函数，应根据实际背景中的变量的实际意义确定.

例3　求函数f（x）＝的定义域.

解　要使函数f（x）有意义，必须满足

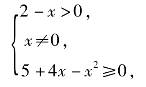
即

(www.daowen.com)

因此函数f（x）的定义域为［－1，0）∪（0，）

2.

函数的表示法通常有三种：解析法、列表法和图象法，三种表示函数的方法各有优缺点.解析法：即借助于数学表达式来表示两个变量之间的函数关系，用解析法表示函数简单明了，但有时在求函数值时较为复杂；列表法：即把函数自变量的取值和其相对应的函数值用一个表格来列出表示，这种表示函数的方法使查询函数值方便，但由于很多函数的自变量取值无法全部列出而导致函数值不完备，且从表中不能直接看出变量间的对应规律，所以局限性较大；图象法：图象法是研究函数性质最为直观的一种表示方法，但在求函数值时不够精确.

2.分段函数

在用解析法表示函数时，有些函数在整个定义域范围内，可以用一个数学式子表示，但有些函数在其定义域的不同部分用不同数学式子才能表示，这类函数称为分段函数.

例4　函数y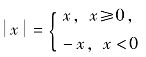＝称为绝对值函数，它的定义域为（－∞，＋∞），值域为[0，＋∞），它的图象如图1.2所示.

例5　函数y＝sgnx＝称为符号函数，它的定义域为（－∞，＋∞），值域为{－1，0，1}，它的图象如图1.3所示.

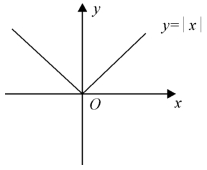
图1.2

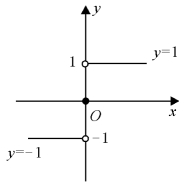
图1.3

例6　函数y＝f（x）＝[x]＝n，n≤x＜n＋1称为取整函数，其中n为整数，记号[x]表示不超过x的最大整数，例如，，[π]＝3，[－1]＝－1，[－4.6]＝－5.

显然，函数y＝[x]的定义域为（－∞＋∞），值域为全体整数，它的图象如图1.4所示，这图形称为阶梯曲线，在x为整数值处，图形发生跳跃，跃度为1.

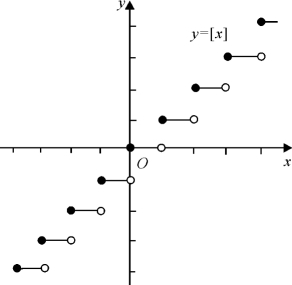
图1.4

3.反函数

在函数中，自变量与因变量的地位是相对的，任意一个变量都可根据需要作为自变量.例如，在函数y＝x＋5中，x是自变量，y是因变量，根据这个式子，可以得到函数x＝y－5，这里y是自变量，x是因变量.上面两个式子反映了同一个过程中两个变量之间地位的相对性，称它们互为反函数.

下面给出反函数的具体定义.

定义2　设函数y＝f（x），其定义域为D，值域为M，且函数y＝f（x）中的“f”为一一对应.如果对于M中的每一个y值，都可从关系式y＝f（x）中找到确定的x值（x∈D）与之对应，那么由此所确定的以y为自变量的新函数叫作y＝f（x）的反函数，记为x＝φ（y）或y＝f－1（x），它的定义域为M，值域为D.

从反函数的定义可以看到，原函数的定义域恰好是其反函数的值域，值域恰好是其反函数的定义域.按照对应法则f，D与M之间必须是一一对应的，所以为使函数y＝f（x）的反函数存在，只要函数y＝f（x）在D上是单调的.下面给出反函数存在定理.

定理（反函数存在定理）　若函数y＝f（x）在定义域上单调增加（或单调减少），则其反函数存在，且其反函数与该函数具有相同的单调性.

在同一直角坐标系中，函数y＝f（x）的图形与反函数y＝f－1（x）的图形关于直线y＝x对称，如图1.5所示.

图1.5